Advertisements
Advertisements
प्रश्न
Write the linear equation such that each point on its graph has an ordinate 3 times its abscissa.
उत्तर
Let abscissa and ordinate of the point be x and y respectively.
According to the question, we have
Ordinate (y) = 3 × abscissa ⇒ y = 3x
When x = 1, then y = 3
When x = 2, then y = 6
| x | 1 | 2 |
| y | 3 | 6 |
Here, we find two points A(1, 3) and B(2, 6).
So, draw the graph by plotting these points and joining them.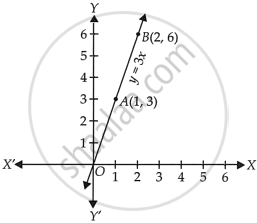
Hence, y = 3x is the required linear equation.
APPEARS IN
संबंधित प्रश्न
The taxi fare in a city is as follows:- For the first kilometre, the fare is Rs. 8 and for the subsequent distance it is Rs. 5 per km. Taking the distance covered as x km and total fare as Rs y, write a linear equation for this information, and draw its graph.
If the point (2, -2) lies on the graph of the linear equation 5x + ky = 4, find the value of k.
Draw the graph of the equatio ` x / y + y /4 = 1` Also, find the area of the triangle formed by the
line and the co-ordinates axes.
Draw the graph obtained from the table below:
| X | a | 3 | - 5 | 5 | c | - 1 |
| Y | - 1 | 2 | b | 3 | 4 | 0 |
Use the graph to find the values of a, b and c. State a linear relation between the variables x and y.
Use the graphical method to find the value of k, if:
(k, -3) lies on the straight line 2x + 3y = 1
Solve, graphically, the following pairs of equations :
`(x + 1)/(4) = (2)/(3)(1 - 2y)`
`(2 + 5y)/(3) = x/(7) -2`
Draw the graph of the equation
y = 5x - 4 Find graphically
a. the value of x, when y = 1
b. the value of y, when x = -2
The point (0, 3) lies on the graph of the linear equation 3x + 4y = 12.
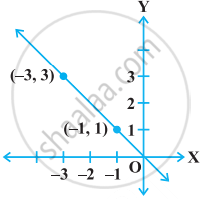
The graph given below represents the linear equation x + y = 0.
Show that the points A(1, 2), B(– 1, – 16) and C(0, – 7) lie on the graph of the linear equation y = 9x – 7.
