Advertisements
Advertisements
Question
Write the linear equation such that each point on its graph has an ordinate 3 times its abscissa.
Solution
Let abscissa and ordinate of the point be x and y respectively.
According to the question, we have
Ordinate (y) = 3 × abscissa ⇒ y = 3x
When x = 1, then y = 3
When x = 2, then y = 6
| x | 1 | 2 |
| y | 3 | 6 |
Here, we find two points A(1, 3) and B(2, 6).
So, draw the graph by plotting these points and joining them.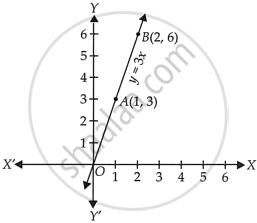
Hence, y = 3x is the required linear equation.
APPEARS IN
RELATED QUESTIONS
Draw the graph for the equation, given below :
x + 5 = 0
Draw the graph for the equation, given below :
y = 7
Use the table given below to draw the graph.
| X | - 5 | - 1 | 3 | b | 13 |
| Y | - 2 | a | 2 | 5 | 7 |
From your graph, find the values of 'a' and 'b'.
State a linear relationship between the variables x and y.
A straight line passes through the points (2, 4) and (5, - 2). Taking 1 cm = 1 unit; mark these points on a graph paper and draw the straight line through these points. If points (m, - 4) and (3, n) lie on the line drawn; find the values of m and n.
Use the graphical method to find the value of k, if:
(5, k - 2) lies on the straight line x - 2y + 1 = 0
Use graph paper for this question. Take 2 cm = 2 units on x-axis and 2 cm = 1 unit on y-axis.
Solve graphically the following equation:
3x + 5y = 12; 3x - 5y + 18 = 0 (Plot only three points per line)
Draw the graph of the equation 4x - 3y + 12 = 0.
Also, find the area of the triangle formed by the line drawn and the coordinate axes.
Use the given table and draw the graph of a straight line.
| X | 1 | 2 | 3 | P |
| Y | 1 | q | -5 | 7 |
Find graphically the values of 'p' and 'q'.
Draw the graph of the following equation:
y = 6
Draw the graph of y = x – 4
