Advertisements
Advertisements
प्रश्न
Draw a pair of vertically opposite angles. Bisect each of the two angles. Verify that the bisecting rays are in the same line.
उत्तर
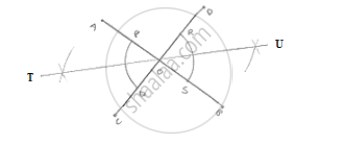
Steps of construction:
1. Draw a pair of vertically opposite angle AOC and DOB
2. With center O and any radius drawn two arcs which intersect OA at P, Q-OB at S and OD at R.
3. With center P and Q and radius more than `1/2`PQ draw two arcs which intersect each other at 7.
4. Join to
5. With center R and S radius more than `1/2`RS, draw two arcs which intersect each other at U.
6. Join OU.
∴ TOU is a straight line
APPEARS IN
संबंधित प्रश्न
Construct an angle of 90° at the initial point of a given ray and justify the construction.
Construct the 75° angles and verify by measuring it by a protractor.
Construct an equilateral triangle, given its side and justify the construction.
Draw a circle with centre at point O and radius 5 cm. Draw its chord AB, draw the
perpendicular bisector of line segment AB. Does it pass through the centre of the circle?
7. Draw a line segment AB and by ruler and compasses1 obtain a line segment of length `3/4`AB.
Draw a linear pair of angles. Bisect each of the two angles. Verify that the two bisecting rays are perpendicular to each other.
Using ruler and compasses only, draw a right angle.
Using a protractor, draw an angle of measure 72°. With this angle as given, draw angles of measure 36° and 54°.
Construct the following angles at the initial point of a given ray and justify the construction 90°.
Construct the angle of the measurement:
1 . 105°
