Advertisements
Advertisements
प्रश्न
Draw the graph of the equation 2x - 3y - 5 = 0
From the graph, find:
(i) x1, the value of x, when y = 7
(ii) x2, the value of x, when y = - 5.
उत्तर
2x - 3y - 5 = 0
⇒ 2x = 3y + 5
⇒ x = `(3y + 5)/(2)`
When y = 1,
x = `(3(1)+5)/(2)`
= `(8)/(2)`
= 4
When y = 3,
x = `(3(3)+5)/(2)`
= `(9 + 5)/(2)`
= 7
When y = - 1,
x = `(3(-1)+5)/(2)`
= `(5 - 3)/(2)`
= 1
| X | 4 | 7 | 1 |
| Y | 1 | 3 | - 1 |
Plotting these points we get the required graph as shown below:

(i) The value of x, when y = 7:
We have the equation of the line as
x = `(3y + 5)/(2)`
Now substitute y = 7 and x = x1:
x1 = `(3(7) + 5)/(2)`
= `(21 + 5)/(2)`
= `(26)/(2)`
= 13
(ii) The value of x, when y = - 5:
Now substitute y = - 5 and x = x2
x2 = `(3(-5) + 5)/(2)`
= `(-15 + 5)/(2)`
= `(-10)/(2)`
= -5.
APPEARS IN
संबंधित प्रश्न
From the choices given below, choose the equation whose graph is given in fig. below.
(i) y = x + 2 (ii) y = x – 2 (iii) y = −x + 2 (iv) x + 2y = 6
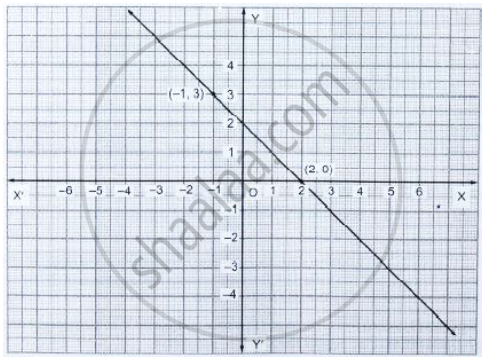
[Hint: Clearly, (2, 0) and (−1, 3) satisfy the equation y = −x + 2]
If the point (2, -2) lies on the graph of the linear equation 5x + ky = 4, find the value of k.
Draw the graph of the equation given below. Also, find the coordinates of the point
where the graph cuts the coordinate axes : −x + 4y = 8
Draw the graph of the equation given below. Also, find the coordinates of the point
where the graph cuts the coordinate axes : 2x + y = 6
Draw the graph of the equation 2x + y = 6. Shade the region bounded by the graph and the
coordinate axes. Also, find the area of the shaded region.
Draw the graph of the equatio ` x / y + y /4 = 1` Also, find the area of the triangle formed by the
line and the co-ordinates axes.
Draw the graph for the equation, given below :
5x + y + 5 = 0
Use graph paper for this question. Take 2 cm = 2 units on x-axis and 2 cm = 1 unit on y-axis.
Solve graphically the following equation:
3x + 5y = 12; 3x - 5y + 18 = 0 (Plot only three points per line)
By drawing a graph for each of the equations 3x + y + 5 = 0; 3y - x = 5 and 2x + 5y = 1 on the same graph paper; show that the lines given by these equations are concurrent (i.e. they pass through the same point). Take 2 cm = 1 unit on both the axes.
The following observed values of x and y are thought to satisfy a linear equation. Write the linear equation:
| x | 6 | – 6 |
| y | –2 | 6 |
Draw the graph using the values of x, y as given in the above table. At what points the graph of the linear equation
- cuts the x-axis
- cuts the y-axis
