Question

The following observed values of x and y are thought to satisfy a linear equation. Write the linear equation:

x	6	– 6
y	–2	6

Draw the graph using the values of x, y as given in the above table. At what points the graph of the linear equation

1. cuts the x-axis
2. cuts the y-axis

Answer 1

Given, points are (6, –2) and (–6, 6).

Let the linear equation y = mx + c is satisfied by the points (6, –2) and (–6, 6), then at point (6, –2)

–2 = 6m + c  ...(i)

And at point (–6, 6), 6 = –6m + c  ...(ii)

On subtracting equation (ii) from equation (i), we get

12m = –8 

⇒ `m = (-8)/12`

⇒ `m = -2/3`

On putting the value of m in equation (i), we get

`–2 = 6(-2/3) + c`

–2 = –4 + c

⇒ c = –2 + 4 

⇒ c = 2

On putting m = `-2/3` and c = 2 in linear equation y = mx + c, we get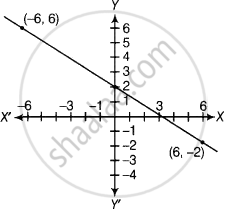

`y = -2/3x + 2`

⇒ `y = (-2x + 6)/3`

⇒ 3y = –2x + 6

⇒ 3y + 2x = 6

When the graph of the linear equation

i. Cuts the x-axis

Then, put y = 0 in equation 2x + 3y = 6, we get

⇒ 2x + 3·0 = 6

⇒ 2x = 6

∴ x = 3

When the graph of the linear equation

ii. Cuts the y-axis

Then, put y = 0 in equation 2x + 3y = 6, we get

⇒ 2·0 + 3y = 6

⇒ 3y = 6

∴ y = 2

Therefore, the graph the linear equation cuts the x-axis at the point (3, 0) and the y-axis at the point (0, 2).