Advertisements
Advertisements
प्रश्न
Draw the graph for each of the following equation: Also, find the coordinates of the points where the graph of the equation meets the coordinate axes:
`(3x + 14)/(2) = (y - 10)/(5)`
उत्तर
`(3x + 14)/(2) = (y - 10)/(5)`
⇒ 15x + 70 = 2y - 20
⇒ 15x - 2y = -90
⇒ 2y = 90 + 15x
⇒ y = `(90 + 15x)/(2)`
Corresponding values of x and y can be tabulated as follows :
| X | -5 | -2 | -1 |
| Y | 7.5 | 30 | 37.5 |
Plotting the points (-5, 7.5), (-2, 30) and (-1, 37.5),
we get the following graph :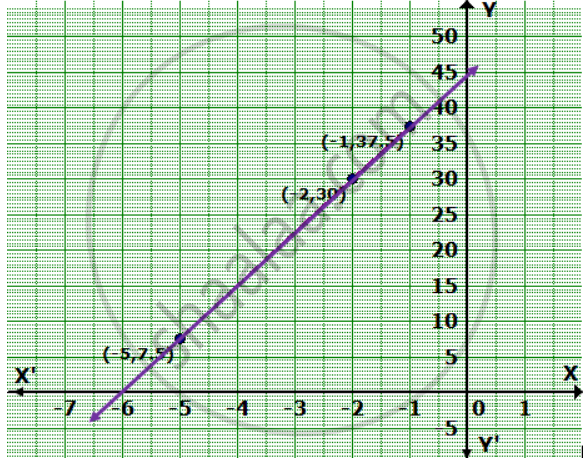
Thus, the graph of the equation meets the X-axis at (-6, 0) and Y-axis at (0, 45).
APPEARS IN
संबंधित प्रश्न
The taxi fare in a city is as follows:- For the first kilometre, the fare is Rs. 8 and for the subsequent distance it is Rs. 5 per km. Taking the distance covered as x km and total fare as Rs y, write a linear equation for this information, and draw its graph.
Draw the graph of the following linear equation in two variable : –x + y = 6
If the point (2, -2) lies on the graph of the linear equation 5x + ky = 4, find the value of k.
Draw the graph of y = | x | + 2.
Solve, graphically, the following pairs of equations :
`(x + 1)/(4) = (2)/(3)(1 - 2y)`
`(2 + 5y)/(3) = x/(7) -2`
Use graph paper for this question. Draw the graph of 2x - y - 1 = 0 and 2x + y = 9 on the same axes. Use 2 cm = 1 unit on both axes and plot only 3 points per line. Write down the coordinates of the point of intersection of the two lines.
Draw the graph of the equation
y = 5x - 4 Find graphically
a. the value of x, when y = 1
b. the value of y, when x = -2
A straight line passes through the points (2, 5) and (-4, -7). Plot these points on a graph paper and draw the straight line passes through these points. If points (a, -1) and (-5, b) lie on the line drawn, find the value of a and b.
Find the values.
2x + y − 6 = 0
| x | 0 | − 1 | ||
| y | 0 | − 2 |
The graph of every linear equation in two variables need not be a line.
