Advertisements
Advertisements
प्रश्न
By drawing a graph for each of the equations 3x + y + 5 = 0; 3y - x = 5 and 2x + 5y = 1 on the same graph paper; show that the lines given by these equations are concurrent (i.e. they pass through the same point). Take 2 cm = 1 unit on both the axes.
उत्तर
3x + y + 5 = 0
⇒ y = - 3x - 5
The table of 3x + y + 5 = 0 is
| X | 1 | - 3 | - 2 |
| Y | - 8 | 4 | 1 |
3y - x = 5
⇒ x = 3y - 5
The table of 3y - x = 5 is
| X | - 2 | 1 | 7 |
| Y | 1 | 2 | 4 |
2x + 5y = 1
⇒ 2x = 1 - 5y
⇒ x = `(1 - 5y)/(2)`
The table of 2x + 5y = 1 is
| X | 3 | - 7 | - 2 |
| Y | - 1 | 3 | 1 |
Plotting the above points, we get the following required graph:
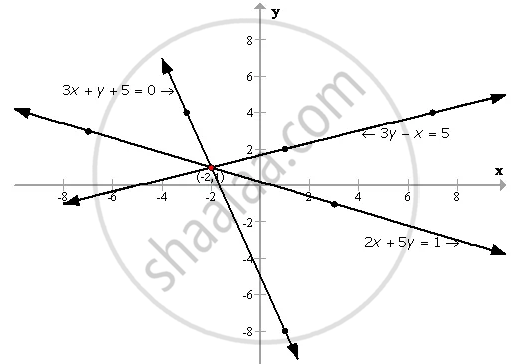
The graph shows that the lines of these equations are concurrent.
APPEARS IN
संबंधित प्रश्न
Draw the graph of the following linear equations in two variables:
x – y = 2
Draw the graph of the following linear equations in two variables:- y = 3x
If the work done by a body on application of a constant force is directly proportional to the distance travelled by the body, express this in the form of an equation in two variables and draw the graph of the same by taking the constant force as 5 units. Also read from the graph the work done when the distance travelled by the body is
(i) 2 units (ii) 0 unit
In countries like USA and Canada, temperature is measured in Fahrenheit, whereas in countries like India, it is measured in Celsius. Here is a linear equation that converts Fahrenheit to Celsius:-
`F=(9/5)C+32`
(i) Draw the graph of the linear equation above using Celsius for x-axis and Fahrenheit for y-axis.
(ii) If the temperature is 30°C, what is the temperature in Fahrenheit?
(iii) If the temperature is 95°F, what is the temperature in Celsius?
(iv) If the temperature is 0°C, what is the temperature in Fahrenheit and if the temperature is 0°F, what is the temperature in Celsius?
(v) Is there a temperature which is numerically the same in both Fahrenheit and Celsius? If yes, find it.
Draw the graph of the following linear equation in two variable : –x + y = 6
Plot the points (3, 5) and (− 1, 3) on a graph paper and verify that the straight line passing
through these points also passes through the point (1, 4).
From the choices given below, choose the equation whose graph is given in Fig. below.
(i) y = x (ii) x + y = 0 (iii) y = 2x (iv) 2 + 3y = 7x

[Hint: Clearly, (-1, 1) and (1, -1) satisfy the equation x + y = 0]
Draw the graph for the equation given below; hence find the co-ordinates of the points where the graph is drawn meets the co-ordinates axes:
`(1)/(3) x +(1)/(5) y = 1`.
The graph given below represents the linear equation x + y = 0.
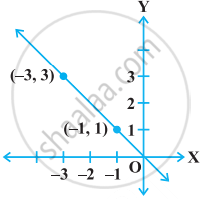
Write the linear equation such that each point on its graph has an ordinate 3 times its abscissa.
