Advertisements
Advertisements
प्रश्न
By drawing a graph for each of the equations 3x + y + 5 = 0; 3y - x = 5 and 2x + 5y = 1 on the same graph paper; show that the lines given by these equations are concurrent (i.e. they pass through the same point). Take 2 cm = 1 unit on both the axes.
उत्तर
3x + y + 5 = 0
⇒ y = - 3x - 5
The table of 3x + y + 5 = 0 is
| X | 1 | - 3 | - 2 |
| Y | - 8 | 4 | 1 |
3y - x = 5
⇒ x = 3y - 5
The table of 3y - x = 5 is
| X | - 2 | 1 | 7 |
| Y | 1 | 2 | 4 |
2x + 5y = 1
⇒ 2x = 1 - 5y
⇒ x = `(1 - 5y)/(2)`
The table of 2x + 5y = 1 is
| X | 3 | - 7 | - 2 |
| Y | - 1 | 3 | 1 |
Plotting the above points, we get the following required graph:
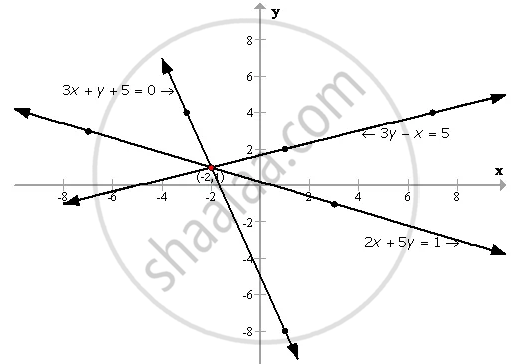
The graph shows that the lines of these equations are concurrent.
APPEARS IN
संबंधित प्रश्न
The taxi fare in a city is as follows:- For the first kilometre, the fare is Rs. 8 and for the subsequent distance it is Rs. 5 per km. Taking the distance covered as x km and total fare as Rs y, write a linear equation for this information, and draw its graph.
Draw the graph of the following linear equation in two variable : 3x + 5y = 15
Draw the graph of the equation given below. Also, find the coordinates of the point
where the graph cuts the coordinate axes : 6x − 3y = 12
Draw the graph for the equation, given below :
x - 5y + 4 = 0
Draw the graph of the equation 4x - 3y + 12 = 0.
Also, find the area of the triangle formed by the line drawn and the coordinate axes.
Draw the graph for the following
y = 2x
Draw the graph for the following
3x + 2y = 14
Find the values.
y = 3x + 1
| x | − 1 | 0 | 1 | 2 |
| y |
The graph of y = 6 is a line ______.
The force exerted to pull a cart is directly proportional to the acceleration produced in the body. Express the statement as a linear equation of two variables and draw the graph of the same by taking the constant mass equal to 6 kg. Read from the graph, the force required when the acceleration produced is (i) 5 m/sec2, (ii) 6 m/sec2.
