Advertisements
Advertisements
प्रश्न
The graph of y = 6 is a line ______.
पर्याय
parallel to x-axis at a distance 6 units from the origin
parallel to y-axis at a distance 6 units from the origin
making an intercept 6 on the x-axis
making an intercept 6 on both the axes
उत्तर
The graph of y = 6 is a line parallel to x-axis at a distance 6 units from the origin.
Explanation:
Given equation of a line can be written as, 0 · x + l · y = 6
To draw the graph of above equation, we need atleast two solutions.
When x = 0, then y = 6
When x = 2, then y = 6
| x | 0 | 2 |
| y | 6 | 6 |
Hence, we find two points A(0, 6) and B(2, 6).
So, draw the graph by plotting these points and joining them, which is shown as follows:
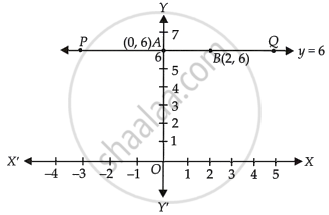
∴ The line PQ parallel to x-axis at a distance 6 units from origin is the required graph of y = 6.
APPEARS IN
संबंधित प्रश्न
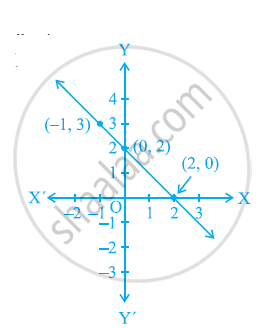
From the choices given below, choose the equation whose graphs are given in the given figures.
For the first figure
(i) y = x
(ii) x + y = 0
(iii) y = 2x
(iv) 2 + 3y = 7x

For the second figure
(i) y = x +2
(ii) y = x − 2
(iii) y = − x + 2
(iv) x + 2y = 6
If the work done by a body on application of a constant force is directly proportional to the distance travelled by the body, express this in the form of an equation in two variables and draw the graph of the same by taking the constant force as 5 units. Also read from the graph the work done when the distance travelled by the body is
(i) 2 units (ii) 0 unit
Draw the graph of the following linear equations in two variable : 2𝑦 = −𝑥 + 1
Draw the graph for the equation, given below :
5x + y + 5 = 0
A straight line passes through the points (2, 4) and (5, - 2). Taking 1 cm = 1 unit; mark these points on a graph paper and draw the straight line through these points. If points (m, - 4) and (3, n) lie on the line drawn; find the values of m and n.
Use the graphical method to find the value of k, if:
(5, k - 2) lies on the straight line x - 2y + 1 = 0
Use graph paper for this question. Draw the graph of 2x - y - 1 = 0 and 2x + y = 9 on the same axes. Use 2 cm = 1 unit on both axes and plot only 3 points per line. Write down the coordinates of the point of intersection of the two lines.
A pair of linear equations has no solution then the graphical representation is
Draw the graph of y = 2x + 5
Draw the graph of the linear equation 3x + 4y = 6. At what points, the graph cuts the x-axis and the y-axis.
