Advertisements
Advertisements
प्रश्न
The graph of y = 6 is a line ______.
विकल्प
parallel to x-axis at a distance 6 units from the origin
parallel to y-axis at a distance 6 units from the origin
making an intercept 6 on the x-axis
making an intercept 6 on both the axes
उत्तर
The graph of y = 6 is a line parallel to x-axis at a distance 6 units from the origin.
Explanation:
Given equation of a line can be written as, 0 · x + l · y = 6
To draw the graph of above equation, we need atleast two solutions.
When x = 0, then y = 6
When x = 2, then y = 6
| x | 0 | 2 |
| y | 6 | 6 |
Hence, we find two points A(0, 6) and B(2, 6).
So, draw the graph by plotting these points and joining them, which is shown as follows:
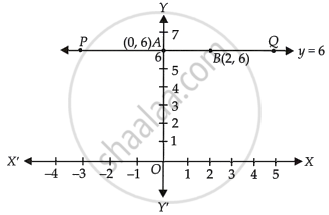
∴ The line PQ parallel to x-axis at a distance 6 units from origin is the required graph of y = 6.
APPEARS IN
संबंधित प्रश्न
Draw the graph of the following linear equations in two variables:- y = 3x
From the choices given below, choose the equation whose graphs are given in the given figures.
For the first figure
(i) y = x
(ii) x + y = 0
(iii) y = 2x
(iv) 2 + 3y = 7x

For the second figure
(i) y = x +2
(ii) y = x − 2
(iii) y = − x + 2
(iv) x + 2y = 6
Draw the graph of the following linear equation in two variable : y = 2x
Draw the graph of the following linear equations in two variable : 2𝑦 = −𝑥 + 1
Draw the graphs of the following linear equations on the same graph paper.
2x + 3y = 12, x – y = 1.
Find the co-ordinates of the vertices of the triangle formed by the two straight lines and the y-axis. Also, find the area of the triangle.
Draw the graph for the equation, given below :
y + 7 = 0
Draw the graph of the straight line given by the equation 4x - 3y + 36 = 0
Calculate the area of the triangle formed by the line drawn and the co-ordinate axes.
Draw the graph of the equation 2x - 3y - 5 = 0
From the graph, find:
(i) x1, the value of x, when y = 7
(ii) x2, the value of x, when y = - 5.
Use graph paper for this question. Take 2 cm = 2 units on x-axis and 2 cm = 1 unit on y-axis.
Solve graphically the following equation:
3x + 5y = 12; 3x - 5y + 18 = 0 (Plot only three points per line)
Draw the graph for each of the following equation: Also, find the coordinates of the points where the graph of the equation meets the coordinate axes:
`(3x + 14)/(2) = (y - 10)/(5)`
