Advertisements
Advertisements
प्रश्न
If the work done by a body on application of a constant force is directly proportional to the distance travelled by the body, express this in the form of an equation in two variables and draw the graph of the same by taking the constant force as 5 units. Also read from the graph the work done when the distance travelled by the body is
(i) 2 units (ii) 0 unit
उत्तर
Let the distance travelled and the work done by the body be x and y respectively.
Work done ∝ distance travelled
y ∝ x
y = kx
Where, k is a constant
If constant force is 5 units, then work done y = 5x
It can be observed that point (1, 5) and (−1, −5) satisfy the above equation. Therefore, these are the solutions of this equation. The graph of this equation is constructed as follows.
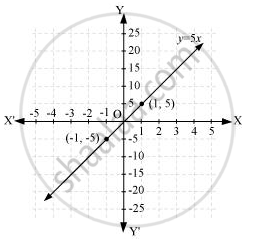
(i)From the graphs, it can be observed that the value of y corresponding to x = 2 is 10. This implies that the work done by the body is 10 units when the distance travelled by it is 2 units.
(ii) From the graphs, it can be observed that the value of y corresponding to x = 0 is 0. This implies that the work done by the body is 0 units when the distance travelled by it is 0 unit.
APPEARS IN
संबंधित प्रश्न
Give the equations of two lines passing through (2, 14). How many more such lines are there, and why?
From the choices given below, choose the equation whose graphs are given in the given figures.
For the first figure
(i) y = x
(ii) x + y = 0
(iii) y = 2x
(iv) 2 + 3y = 7x

For the second figure
(i) y = x +2
(ii) y = x − 2
(iii) y = − x + 2
(iv) x + 2y = 6
Draw the graph of the following linear equations in two variable : 2𝑦 = −𝑥 + 1
Draw the graph for the equation, given below :
x + 5 = 0
Draw the graph (straight line) given by equation x - 3y = 18. If the straight line is drawn passes through the points (m, - 5) and (6, n); find the values of m and n.
Using a scale of 1 cm to 1 unit for both the axes, draw the graphs of the following equations: 6y = 5x + 10, y = 5x - 15.
From the graph find :
(i) the coordinates of the point where the two lines intersect;
(ii) the area of the triangle between the lines and the x-axis.
Draw the graphs of the following linear equations:
3x + 2y - 6 = 0
Find the values.
2x + y − 6 = 0
| x | 0 | − 1 | ||
| y | 0 | − 2 |
Find the values.
y = 3x + 1
| x | − 1 | 0 | 1 | 2 |
| y |
The graph given below represents the linear equation x + y = 0.