Advertisements
Advertisements
Question
By drawing a graph for each of the equations 3x + y + 5 = 0; 3y - x = 5 and 2x + 5y = 1 on the same graph paper; show that the lines given by these equations are concurrent (i.e. they pass through the same point). Take 2 cm = 1 unit on both the axes.
Solution
3x + y + 5 = 0
⇒ y = - 3x - 5
The table of 3x + y + 5 = 0 is
| X | 1 | - 3 | - 2 |
| Y | - 8 | 4 | 1 |
3y - x = 5
⇒ x = 3y - 5
The table of 3y - x = 5 is
| X | - 2 | 1 | 7 |
| Y | 1 | 2 | 4 |
2x + 5y = 1
⇒ 2x = 1 - 5y
⇒ x = `(1 - 5y)/(2)`
The table of 2x + 5y = 1 is
| X | 3 | - 7 | - 2 |
| Y | - 1 | 3 | 1 |
Plotting the above points, we get the following required graph:
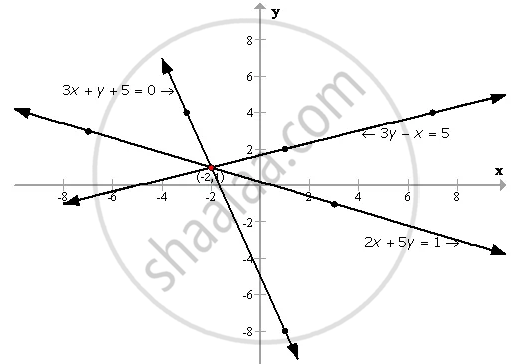
The graph shows that the lines of these equations are concurrent.
APPEARS IN
RELATED QUESTIONS
Yamini and Fatima, two students of Class IX of a school, together contributed Rs. 100 towards the Prime Minister’s Relief Fund to help the earthquake victims. Write a linear equation which satisfies this data. (You may take their contributions as Rs. x and Rs. y.) Draw the graph of the same.
Draw the graph for the equation, given below :
y + 7 = 0
Draw the graph for each of the following equation: Also, find the coordinates of the points where the graph of the equation meets the coordinate axes:
`(1)/(2) x + (1)/(3) y` = 1
Draw the graph of the equation
y = 5x - 4 Find graphically
a. the value of x, when y = 1
b. the value of y, when x = -2
A straight line passes through the points (2, 5) and (-4, -7). Plot these points on a graph paper and draw the straight line passes through these points. If points (a, -1) and (-5, b) lie on the line drawn, find the value of a and b.
Draw the graph for the following
y = 2x
Draw the graph for the following
y = `(3/2)x + 3`
Find the values.
2x + y − 6 = 0
| x | 0 | − 1 | ||
| y | 0 | − 2 |
The point (0, 3) lies on the graph of the linear equation 3x + 4y = 12.
Draw the graphs of linear equations y = x and y = – x on the same cartesian plane. What do you observe?
