Advertisements
Advertisements
Question
Draw the graphs of linear equations y = x and y = – x on the same cartesian plane. What do you observe?
Solution
The given equation is y = x. To draw the graph of this equation, we need at least two points lying on the given line.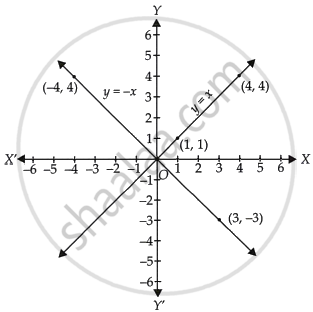
For x = 1, y = 1, therefore (1, 1) satisfies the linear equation y = x.
For x = 4, y = 4, therefore (4, 4) satisfies the linear equation y = x.
By plotting the points (1, 1) and (4, 4) on the graph paper and joining them by a line, we obtain the graph of y = x.
The given equation is y = – x. To draw the graph of this equation, we need at least two points lying on the given line.
For x = 3, y = – 3, therefore, (3, – 3) satisfies the linear equation y = – x.
For x = – 4, y = 4, therefore, (– 4, 4) satisfies the linear equation y = – x.
By plotting the points (3, – 3) and (– 4, 4) on the graph paper and joining them by a line, we obtain the graph of y = – x.
We observe that, the line y = x and y = – x intersect at the point O(0, 0).
APPEARS IN
RELATED QUESTIONS
In countries like USA and Canada, temperature is measured in Fahrenheit, whereas in countries like India, it is measured in Celsius. Here is a linear equation that converts Fahrenheit to Celsius:-
`F=(9/5)C+32`
(i) Draw the graph of the linear equation above using Celsius for x-axis and Fahrenheit for y-axis.
(ii) If the temperature is 30°C, what is the temperature in Fahrenheit?
(iii) If the temperature is 95°F, what is the temperature in Celsius?
(iv) If the temperature is 0°C, what is the temperature in Fahrenheit and if the temperature is 0°F, what is the temperature in Celsius?
(v) Is there a temperature which is numerically the same in both Fahrenheit and Celsius? If yes, find it.
Draw the graph of the following linear equation in two variable : ` x / 2 - y/ 3 = 2`
Draw the graph for the equation given below; hence find the co-ordinates of the points where the graph is drawn meets the co-ordinates axes:
`(2x + 15)/(3) = y - 1`
Draw the graph of the following equation:
x = – 7
Draw the graph of the following equation:
y = 6
Draw the graph of y = x – 4
The graph given below represents the linear equation x + y = 0.
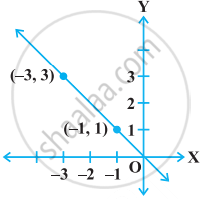
The graph given below represents the linear equation x = 3 (see figure).

Every point on the graph of a linear equation in two variables does not represent a solution of the linear equation.
The following observed values of x and y are thought to satisfy a linear equation. Write the linear equation:
| x | 6 | – 6 |
| y | –2 | 6 |
Draw the graph using the values of x, y as given in the above table. At what points the graph of the linear equation
- cuts the x-axis
- cuts the y-axis
