Advertisements
Advertisements
Question
Draw the graph for the equation given below; hence find the co-ordinates of the points where the graph is drawn meets the co-ordinates axes:
`(2x + 15)/(3) = y - 1`
Solution
`(2x + 15)/(3) = y - 1`
⇒ 2x + 15 = 3(y - 1)
⇒ 2x + 15 = 3y - 3
⇒ 2x - 3y = -15 - 3
⇒ 2x - 3y = -18
⇒ -3y = -18 - 2x
⇒ y = `(-18 - 2x)/(-3)`
When x = 0,
y = `(-18-[2 xx 0])/(-3)`
= `(-18 -0)/(-3)`
= 6
When x = -3,
y = `(-18-[2 xx (-3)])/(-3)`
= `(-18 + 6)/(-3)`
= 4
When x = -6,
y = `(-18-[2 xx (-6)])/(-3)`
= `(-18 + 12)/(-3)`
= 2
| X | 0 | - 3 | - 6 |
| Y | 6 | 4 | 2 |
Plotting these points we get the required graph as shown below:
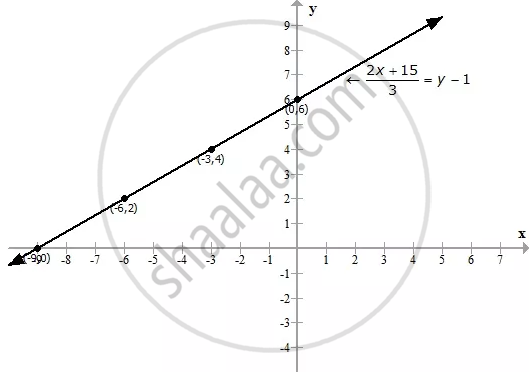
From the figure it is clear that, the graph meets the coordinate axes at (-9, 0) and (0, 6).
APPEARS IN
RELATED QUESTIONS
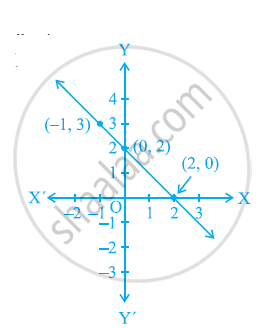
From the choices given below, choose the equation whose graphs are given in the given figures.
For the first figure
(i) y = x
(ii) x + y = 0
(iii) y = 2x
(iv) 2 + 3y = 7x

For the second figure
(i) y = x +2
(ii) y = x − 2
(iii) y = − x + 2
(iv) x + 2y = 6
Draw the graph of the following linear equation in two variable : 3x + 5y = 15
Draw the graph of the equation given below. Also, find the coordinates of the point
where the graph cuts the coordinate axes : 2x + y = 6
Draw the graph for the equation, given below :
y = 7
Draw the graph for the equation, given below :
x - 5y + 4 = 0
Use the table given below to draw the graph.
| X | - 5 | - 1 | 3 | b | 13 |
| Y | - 2 | a | 2 | 5 | 7 |
From your graph, find the values of 'a' and 'b'.
State a linear relationship between the variables x and y.
Draw the graph for each of the following equation: Also, find the coordinates of the points where the graph of the equation meets the coordinate axes:
`(3x + 14)/(2) = (y - 10)/(5)`
Draw the graph for the following
y = 4x – 1
Draw the graph of y = – 3x
Find the values.
y = x + 3
| x | 0 | − 2 | ||
| y | 0 | − 3 |
