Advertisements
Advertisements
Question
Draw the graph for the equation, given below :
x - 5y + 4 = 0
Solution
x - 5y + 4 = 0
⇒ 5y = 4 + x
∴ y = `(x + 4)/(5)`
When x = 1;
y = `(1 + 4)/(5)`
= `(5)/(5)`
= 1
When x = 6;
y = `(6 + 4)/(5)`
= `(10)/(5)`
= 2
When x = - 4;
y = `(-4 + 4)/(5)`
= `(0)/(5)`
= 0
| X | 1 | 6 | - 4 |
| Y | 1 | 2 | 0 |
Plotting these points we get the required graph as shown below :
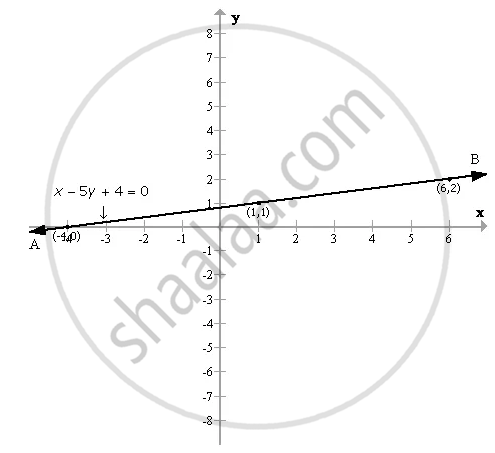
APPEARS IN
RELATED QUESTIONS
If the point (2, -2) lies on the graph of the linear equation 5x + ky = 4, find the value of k.
Draw the graph of the equation given below. Also, find the coordinate of the points
where the graph cuts the coordinate axes : 3x + 2y + 6 = 0
Draw the graph for the equation, given below :
x + 5 = 0
Solve, graphically, the following pairs of equation :
2x + y = 23
4x - y = 19
A straight line passes through the points (2, 5) and (-4, -7). Plot these points on a graph paper and draw the straight line passes through these points. If points (a, -1) and (-5, b) lie on the line drawn, find the value of a and b.
Draw the graph of y = – 3x
Find the values.
2x + y − 6 = 0
| x | 0 | − 1 | ||
| y | 0 | − 2 |
The graph of the linear equation 2x + 3y = 6 is a line which meets the x-axis at the point ______.
Write the linear equation such that each point on its graph has an ordinate 3 times its abscissa.
The following observed values of x and y are thought to satisfy a linear equation. Write the linear equation:
| x | 6 | – 6 |
| y | –2 | 6 |
Draw the graph using the values of x, y as given in the above table. At what points the graph of the linear equation
- cuts the x-axis
- cuts the y-axis
