Advertisements
Advertisements
Question
Draw the graph for the following
y = `(3/2)x + 3`
Solution
When x = −2,
y = `3/2(- 2) + 3`
y = −3 + 3 = 0
when x = 0,
y = `3/2(0) + 3`
y = 3
when x = 2,
y = `3/2(2) + 3`
y = 3 + 3
= 6
| x | −2 | 0 | 2 |
| y | 0 | 3 | 6 |
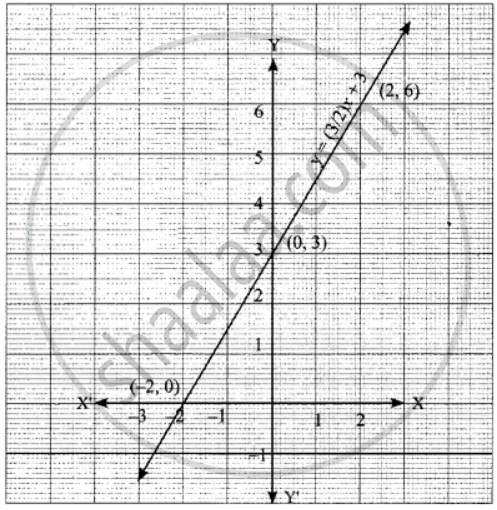
Plot the points (−2, 0) (0, 3) and (2, 6) in the graph sheet we get a straight line.
APPEARS IN
RELATED QUESTIONS
Yamini and Fatima, two students of Class IX of a school, together contributed Rs. 100 towards the Prime Minister’s Relief Fund to help the earthquake victims. Write a linear equation which satisfies this data. (You may take their contributions as Rs. x and Rs. y.) Draw the graph of the same.
Draw the graph of the following linear equation in two variable : y = 2x
Draw the graph of the equatio ` x / y + y /4 = 1` Also, find the area of the triangle formed by the
line and the co-ordinates axes.
Draw the graph for the equation, given below :
3x + 2y = 6
Solve, graphically, the following pairs of equation :
3x + 7y = 27
8 - y = `(5)/(2)x`
Use graph paper for this question. Draw the graph of 2x - y - 1 = 0 and 2x + y = 9 on the same axes. Use 2 cm = 1 unit on both axes and plot only 3 points per line. Write down the coordinates of the point of intersection of the two lines.
A straight line passes through the points (2, 5) and (-4, -7). Plot these points on a graph paper and draw the straight line passes through these points. If points (a, -1) and (-5, b) lie on the line drawn, find the value of a and b.
Find the values.
y = 3x + 1
| x | − 1 | 0 | 1 | 2 |
| y |
The graph of the linear equation x + 2y = 7 passes through the point (0, 7).
The force exerted to pull a cart is directly proportional to the acceleration produced in the body. Express the statement as a linear equation of two variables and draw the graph of the same by taking the constant mass equal to 6 kg. Read from the graph, the force required when the acceleration produced is (i) 5 m/sec2, (ii) 6 m/sec2.
