Advertisements
Chapters
![Samacheer Kalvi solutions for Mathematics [English] Class 9 TN Board chapter 3 - Algebra Samacheer Kalvi solutions for Mathematics [English] Class 9 TN Board chapter 3 - Algebra - Shaalaa.com](/images/mathematics-english-class-9-tn-board_6:5f2b1b2038084cf381bfa42c826a928c.jpg)
Advertisements
Solutions for Chapter 3: Algebra
Below listed, you can find solutions for Chapter 3 of Tamil Nadu Board of Secondary Education Samacheer Kalvi for Mathematics [English] Class 9 TN Board.
Samacheer Kalvi solutions for Mathematics [English] Class 9 TN Board 3 Algebra Exercise 3.1 [Pages 87 - 88]
Identify the following expression is polynomial. If not give reason:
`1/x^2 + 3x - 4`
Identify the following expression is polynomial. If not give reason:
x2(x – 1)
Identify the following expression is polynomial. If not give reason:
`1/x(x + 5)`
Identify the following expression is polynomial. If not give reason:
`1/(x^(-2)) + 1/(x^(-1)) + 7`
Identify the following expression is polynomial. If not give reason:
`sqrt(5)x^2 + sqrt(3)x + sqrt(2)`
Identify the following expression is polynomial. If not give reason:
`"m"^2 - root(3)("m") + 7"m" - 10`
Write the coefficient of x2 and x in the following polynomials
`4 + 2/5x^2 - 3x`
Write the coefficient of x2 and x in the following polynomials
`6 - 2x^2 + 3x^3 - sqrt(7)x`
Write the coefficient of x2 and x in the following polynomials
πx2 – x + 2
Write the coefficient of x2 and x in the following polynomials
`sqrt(3)x^2 + sqrt(2)x + 0.5`
Find the degree of the following polynomial
`2sqrt(5)"p"^4 - (8"p"^3)/sqrt(3) + (2"p"^2)/7`
Write the coefficient of x2 and x in the following polynomials
`x^2 - 7/2 x + 8`
Find the degree of the following polynomial
`1 - sqrt(2)y^2 + y^7`
Find the degree of the following polynomial
`(x^3 - x^4 + 6x^6)/x^2`
Find the degree of the following polynomial
x3(x2 + x)
Find the degree of the following polynomial
3x4 + 9x2 + 27x6
Rewrite the following polynomial in standard form
`x - 9 + sqrt(7)x^3 + 6x^2`
Rewrite the following polynomial in standard form
`sqrt(2)x^2 - 7/2 x^4 + x - 5x^3`
Rewrite the following polynomial in standard form
`7x^3 - 6/5x^2 + 4x - 1`
Rewrite the following polynomial in standard form
`y^2 + sqrt(5)y^3 - 11 - 7/3y + 9y^4`
Add the following polynomials and find the degree of the resultant polynomial
p(x) = 6x2 – 7x + 2, q(x) = 6x3 – 7x + 15
Add the following polynomials and find the degree of the resultant polynomial
h(x) = 7x3 – 6x + 1, f(x) = 7x2 + 17x – 9
Add the following polynomials and find the degree of the resultant polynomial
f(x) = 16x4 – 5x2 + 9, g(x) = −6x3 + 7x – 15
Subtract the second polynomial from the first polynomial and find the degree of the resultant polynomial
p(x) = 7x2 + 6x – 1, q(x) = 6x – 9
Subtract the second polynomial from the first polynomial and find the degree of the resultant polynomial
f(y) = 6y2 – 7y + 2, g(y) = 7y + y3
Subtract the second polynomial from the first polynomial and find the degree of the resultant polynomial
h(z) = z5 – 6z4 + z, f(z) = 6z2 + 10z – 7
What should be added to 2x3 + 6x2 – 5x + 8 to get 3x3 – 2x2 + 6x + 15?
What must be subtracted from 2x4 + 4x2 – 3x + 7 to get 3x3 – x2 + 2x + 1?
Multiply the following polynomials and find the degree of the resultant polynomial:
p(x) = x2 – 9, q(x) = 6x2 + 7x – 2
Multiply the following polynomials and find the degree of the resultant polynomial:
f(x) = 7x + 2, g(x) = 15x – 9
Multiply the following polynomials and find the degree of the resultant polynomial:
h(x) = 6x2 – 7x + 1, f(x) = 5x – 7
The cost of a chocolate is Rs. (x + y) and Amir bought (x + y) chocolates. Find the total amount paid by him in terms of x and y. If x = 10, y = 5 find the amount paid by him
The length of a rectangle is (3x + 2) units and it’s breadth is (3x – 2) units. Find its area in terms of x. What will be the area if x = 20 units
p(x) is a polynomial of degree 1 and q(x) is a polynomial of degree 2. What kind of the polynomial is p(x) × q(x)?
Samacheer Kalvi solutions for Mathematics [English] Class 9 TN Board 3 Algebra Exercise 3.2 [Pages 91 - 92]
Find the value of the polynomial f(y) = 6y – 3y2 + 3 at y = 1
Find the value of the polynomial f(y) = 6y – 3y2 + 3 at y = –1
Find the value of the polynomial f(y) = 6y – 3y2 + 3 at y = 0
If p(x) = `x^2 - 2sqrt(2)x + 1`, find `"p"(2sqrt(2))`
Find the zero of the polynomial of the following:
p(x) = x – 3
Find the zero of the polynomial of the following:
p(x) = 2x + 5
Find the zero of the polynomial of the following:
q(y) = 2y – 3
Find the zero of the polynomial of the following :
f(z) = 8z
Find the zero of the polynomial in the following:
h(x) = ax + b, a ≠ 0, a, b ∈ R
Find the zero of the polynomial of the following:
p(x) = ax when a ≠ 0
Find the roots of the polynomial equation
5x – 6 = 0
Find the roots of the polynomial equation
x + 3 = 0
Find the roots of the polynomial equation
10x + 9 = 0
Find the roots of the polynomial equation
9x – 4 = 0
Verify whether the following are zeros of the polynomial indicated against them, or not
p(x) = 2x − 1, x = `1/2`
Verify whether the following are zeros of the polynomial, indicated against them, or not
p(x) = x3 – 1, x = 1
Verify whether the following are zeros of the polynomial, indicated against them, or not
p(x) = ax + b, x = `(-"b")/"a"`
Verify whether the following are zeros of the polynomial, indicated against them, or not
p(x) = (x + 3) (x – 4), x = −3, x = 4
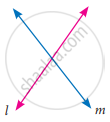
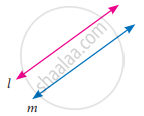
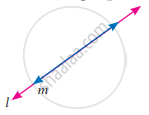
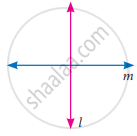
Find the number of zeros of the following polynomial represented by their graph
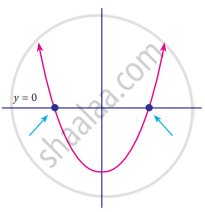
Find the number of zeros of the following polynomial represented by their graph
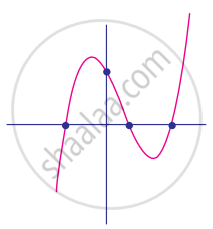
Find the number of zeros of the following polynomial represented by their graph
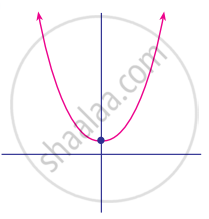
Find the number of zeros of the following polynomial represented by their graph
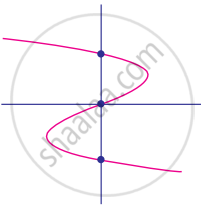
Find the number of zeros of the following polynomial represented by their graph
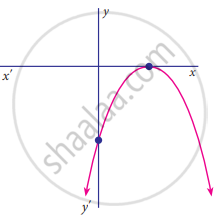
Samacheer Kalvi solutions for Mathematics [English] Class 9 TN Board 3 Algebra Exercise 3.3 [Pages 96 - 97]
Check whether p(x) is a multiple of g(x) or not
p(x) = x3 – 5x2 + 4x – 3, g(x) = x – 2
By remainder theorem, find the remainder when, p(x) is divided by g(x) where, p(x) = x3 – 2x2 – 4x – 1; g(x) = x + 1
By remainder theorem, find the remainder when, p(x) is divided by g(x) where, p(x) = 4x3 – 12x2 + 14x – 3; g(x) = 2x – 1
By remainder theorem, find the remainder when, p(x) is divided by g(x) where, p(x) = x3 – 3x2 + 4x + 50; g(x) = x – 3
Find the remainder when 3x3 – 4x2 + 7x – 5 is divided by (x + 3)
What is the remainder when x2018 + 2018 is divided by x – 1
For what value of k is the polynomial p(x) = 2x3 – kx2 + 3x + 10 exactly divisible by (x – 2)
If two polynomials 2x3 + ax2 + 4x – 12 and x3 + x2 – 2x + a leave the same remainder when divided by (x – 3), find the value of a and also find the remainder.
Determine whether (x – 1) is a factor of the following polynomials:
x3 + 5x2 – 10x + 4
Determine whether (x – 1) is a factor of the following polynomials:
x4 + 5x2 – 5x + 1
Using factor theorem, show that (x – 5) is a factor of the polynomial
2x3 – 5x2 – 28x + 15
Determine the value of m, if (x + 3) is a factor of x3 – 3x2 – mx + 24
If both (x − 2) and `(x - 1/2)` is the factors of ax2 + 5x + b, then show that a = b
If (x – 1) divides the polynomial kx3 – 2x2 + 25x – 26 without remainder, then find the value of k
Check if (x + 2) and (x – 4) are the sides of a rectangle whose area is x2 – 2x – 8 by using factor theorem
Samacheer Kalvi solutions for Mathematics [English] Class 9 TN Board 3 Algebra Exercise 3.4 [Pages 101 - 102]
Expand the following:
(2x + 3y + 4z)2
Expand the following:
(−p + 2q + 3r)2
Expand the following:
(2p + 3)(2p – 4)(2p – 5)
Expand the following:
(3a + 1)(3a – 2)(3a + 4)
Using algebraic identity, find the coefficients of x2, x and constant term without actual expansion
(x + 5)(x + 6)(x + 7)
Using algebraic identity, find the coefficients of x2, x and constant term without actual expansion
(2x + 3)(2x – 5)(2x – 6)
If (x + a)(x + b)(x + c) = x3 + 14x2 + 59x + 70, find the value of a + b + c
If (x + a)(x + b)(x + c) = x3 + 14x2 + 59x + 70, find the value of `1/"a" + 1/"b" + 1/"c"`
If (x + a)(x + b)(x + c) = x3 + 14x2 + 59x + 70, find the value of a2 + b2 + c2
If (x + a)(x + b)(x + c) = x3 + 14x2 + 59x + 70, find the value of `"a"/"bc" + "b"/"ac" + "c"/"ab"`
Expand: (3a – 4b)3
Expand: `[x + 1/y]^3`
Evaluate the following by using identities:
983
Evaluate the following by using identities:
10013
If (x + y + z) = 9 and (xy + yz + zx) = 26, then find the value of x2 + y2 + z2
Find 27a3 + 64b3, if 3a + 4b = 10 and ab = 2
Find x3 – y3, if x – y = 5 and xy = 14.
If `"a" + 1/"a"` = 6, then find the value of `"a"^3 + 1/"a"^3`
If `x^2 + 1/x^2` = 23, then find the value of `x + 1/x` and `x^3 + 1/x^3`
If `(y - 1/y)^3` = 27, then find the value of `y^3 - 1/y^3`
Simplify: (2a + 3b + 4c) (4a2 + 9b2 + 16c2 – 6ab – 12bc – 8ca)
Simplify: (x – 2y + 3z) (x2 + 4y2 + 9z2 + 2xy + 6yz – 3xz)
By using identity evaluate the following:
73 – 103 + 33
By using identity evaluate the following:
`1 + 1/8 - 27/8`
If 2x – 3y – 4z = 0, then find 8x3 – 27y3 – 64z3
Samacheer Kalvi solutions for Mathematics [English] Class 9 TN Board 3 Algebra Exercise 3.5 [Page 105]
Factorise the following expression:
2a² + 4a²b + 8a²c
Factorise the following expression:
ab – ac – mb + mc
Factorise the following:
x² + 4x + 4
Factorise the following:
3a² – 24ab + 48b²
Factorise the following:
x5 – 16x
Factorise the following:
`"m"^2 + 1/"m"^2 - 23`
Factorise the following:
6 – 216x2
Factorise the following:
`"a"^2 + 1/"a"^2 - 18`
Factorise the following:
4x2 + 9y2 + 25z2 + 12xy + 30yz + 20xz
Factorise the following:
25x2 + 4y2 + 9z2 – 20xy + 12yz – 30xz
Factorise the following:
8x3 + 125y3
Factorise the following:
27x3 – 8y3
Factorise the following:
a6 – 64
Factorise the following:
x3 + 8y3 + 6xy – 1
Factorise the following:
l3 – 8m3 – 27n3 – 18lmn
Samacheer Kalvi solutions for Mathematics [English] Class 9 TN Board 3 Algebra Exercise 3.6 [Page 107]
Factorise the following:
x² + 10x + 24
Factorise the following:
z² + 4z – 12
Factorise the following:
p² – 6p – 16
Factorise the following:
t² + 72 – 17t
Factorise the following:
y2 – 16y – 80
Factorise the following:
a2 + 10a – 600
Factorise the following:
2a2 + 9a + 10
Factorise the following:
5x2 – 29xy – 42y2
Factorise the following:
9 – 18x + 8x2
Factorise the following:
6x2 + 16xy + 8y2
Factorise the following:
12x2 + 36x2y + 27y2x2
Factorise the following:
(a + b)2 + 9(a + b) + 18
Factorise the following:
(p – q)2 – 6(p – q) – 16
Factorise the following:
m2 + 2mn – 24n2
Factorise the following:
`sqrt(5)"a"^2 + 2"a" - 3sqrt(5)`
Factorise the following:
a4 – 3a2 + 2
Factorise the following:
8m3 – 2m2n – 15mn2
Factorise the following:
`1/x^2 + 1/y^2 + 2/(xy)`
Samacheer Kalvi solutions for Mathematics [English] Class 9 TN Board 3 Algebra Exercise 3.7 [Pages 111 - 112]
Find the quotient and remainder of the following.
(4x3 + 6x2 – 23x + 18) ÷ (x + 3)
Find the quotient and remainder of the following.
(8y3 – 16y2 + 16y – 15) ÷ (2y – 1)
Find the quotient and remainder of the following.
(8x3 – 1) ÷ (2x – 1)
Find the quotient and remainder of the following.
(−18z + 14z2 + 24z3 + 18) ÷ (3z + 4)
The area of a rectangle is x2 + 7x + 12. If its breadth is (x + 3), then find its length
The base of a parallelogram is (5x + 4). Find its height if the area is 25x2 – 16
The sum of (x + 5) observations is (x3 + 125). Find the mean of the observations
Find the quotient and remainder for the following using synthetic division:
(x3 + x2 – 7x – 3) ÷ (x – 3)
Find the quotient and remainder for the following using synthetic division:
(x3 + 2x2 – x – 4) ÷ (x + 2)
Find the quotient and remainder for the following using synthetic division:
(3x3 – 2x2 + 7x – 5) ÷ (x + 3)
Find the quotient and remainder for the following using synthetic division:
(8x4 – 2x2 + 6x + 5) ÷ (4x + 1)
If the quotient obtained on dividing (8x4 – 2x2 + 6x – 7) by (2x + 1) is (4x3 + px2 – qx + 3), then find p, q and also the remainder
If the quotient obtained on dividing 3x3 + 11x2 + 34x + 106 by x – 3 is 3x2 + ax + b, then find a, b and also the remainder
Samacheer Kalvi solutions for Mathematics [English] Class 9 TN Board 3 Algebra Exercise 3.8 [Page 114]
Factorise the following polynomials using synthetic division:
x3 – 3x2 – 10x + 24
Factorise the following polynomials using synthetic division:
2x3 – 3x2 – 3x + 2
Factorise the following polynomials using synthetic division:
– 7x + 3 + 4x3
Factorise the following polynomials using synthetic division:
x3 + x2 – 14x – 24
Factorise the following polynomials using synthetic division:
x3 – 7x + 6
Factorise the following polynomials using synthetic division:
x3 – 10x2 – x + 10
Samacheer Kalvi solutions for Mathematics [English] Class 9 TN Board 3 Algebra Exercise 3.9 [Page 115]
Find the G.C.D for the following:
P5, P11, P9
Find the G.C.D for the following:
4x3, y3, z3
Find the G.C.D for the following:
9a2b2c3, 15a3b2c4
Find the G.C.D for the following:
64x8, 240x6
Find the G.C.D for the following:
ab2c3, a2b3c, a3bc2
Find the G.C.D for the following:
35x5y3z4, 49x2yz3, 14xy2z2
Find the G.C.D for the following:
25ab3c, 100a2bc, 125ab
Find the G.C.D for the following:
3abc, 5xyz, 7pqr
Find the G.C.D of the following:
(2x + 5), (5x + 2)
Find the G.C.D of the following:
am+1, am+2, am+3
Find the G.C.D of the following:
2a2 + a, 4a2 – 1
Find the G.C.D of the following:
3a2, 5b3, 7c4
Find the G.C.D of the following:
x4 – 1, x2 – 1
Find the G.C.D of the following:
a3 – 9ax2, (a – 3x)2
Samacheer Kalvi solutions for Mathematics [English] Class 9 TN Board 3 Algebra Exercise 3.10 [Page 124]
Draw the graph for the following
y = 2x
Draw the graph for the following
y = 4x – 1
Draw the graph for the following
y = `(3/2)x + 3`
Draw the graph for the following
3x + 2y = 14
Solve graphically
x + y = 7, x – y = 3
Solve graphically
3x + 2y = 4, 9x + 6y – 12 = 0
Solve graphically
`x/2 + y/4` = 1, `x/2 + y/4` = 2
Solve graphically
x – y = 0, y + 3 = 0
Solve graphically
y = 2x + 1, y + 3x – 6 = 0
Solve graphically
x = −3, y = 3
Two cars are 100 miles apart. If they drive towards each other they will meet in 1 hour. If they drive in the same direction they will meet in 2 hours. Find their speed by using graphical method.
Samacheer Kalvi solutions for Mathematics [English] Class 9 TN Board 3 Algebra Exercise 3.11 [Page 126]
Solve, using the method of substitution
2x – 3y = 7, 5x + y = 9
Solve, using the method of substitution
1.5x + 0.1y = 6.2, 3x – 0.4y = 11.2
Solve, using the method of substitution
10% of x + 20% of y = 24, 3x – y = 20
Solve, using the method of substitution
`sqrt(2)x - sqrt(3)y` = 1, `sqrt(3)x - sqrt(8)y` = 0
Raman’s age is three times the sum of the ages of his two sons. After 5 years his age will be twice the sum of the ages of his two sons. Find the age of Raman.
The middle digit of a number between 100 and 1000 is zero and the sum of the other digit is 13. If the digits are reversed, the number so formed exceeds the original number by 495. Find the number
Samacheer Kalvi solutions for Mathematics [English] Class 9 TN Board 3 Algebra Exercise 3.12 [Page 128]
Solve by the method of elimination
2x – y = 3, 3x + y = 7
Solve by the method of elimination
x – y = 5, 3x + 2y = 25
Solve by the method of elimination
`x/10 + y/5` = 14, `x/8 + y/6` = 15
Solve by the method of elimination
3(2x + y) = 7xy, 3(x + 3y) = 11xy
Solve by the method of elimination
`4/x + 5y` = 7, `3/x + 4y` = 5
Solve by the method of elimination
13x + 11y = 70, 11x + 13y = 74
The monthly income of A and B are in the ratio 3 : 4 and their monthly expenditures are in the ratio 5 : 7. If each saves ₹ 5,000 per month, find the monthly income of each
Five years ago, a man was seven times as old as his son, while five year hence, the man will be four times as old as his son. Find their present age
Samacheer Kalvi solutions for Mathematics [English] Class 9 TN Board 3 Algebra Exercise 3.13 [Page 131]
Solve by cross-multiplication method
8x – 3y = 12, 5x = 2y + 7
Solve by cross-multiplication method
6x + 7y – 11 = 0, 5x + 2y = 13
Solve by cross-multiplication method
`2/x + 3/y` = 5, `3/x - 1/y + 9` = 0
Akshaya has 2 rupee coins and 5 rupee coins in her purse. If in all she has 80 coins totalling ₹ 220, how many coins of each kind does she have.
It takes 24 hours to fill a swimming pool using two pipes. If the pipe of larger diameter is used for 8 hours and the pipe of the smaller diameter is used for 18 hours. Only half of the pool is filled. How long would each pipe take to fill the swimming pool
Samacheer Kalvi solutions for Mathematics [English] Class 9 TN Board 3 Algebra Exercise 3.14 [Page 133]
Solve by anyone of the methods
The sum of a two digit number and the number formed by interchanging the digits is 110. If 10 is subtracted from the first number, the new number is 4 more than 5 times the sums of the digits of the first number. Find the first number.
The sum of the numerator and denominator of a fraction is 12. If the denominator is increased by 3, the fraction becomes `1/2`. Find the fraction
ABCD is a cyclic quadrilateral such that ∠A = (4y + 20)°, ∠B = (3y − 5)°, ∠C = (4x)° and ∠D = (7x + 5)°. Find the four angles
On selling a T.V. at 5% gain and a fridge at 10% gain, a shopkeeper gains ₹ 2000. But if he sells the T.V. at 10% gain and the fridge at 5% loss, he gains Rs. 1500 on the transaction. Find the actual price of the T.V. and the fridge.
Two numbers are in the ratio 5 : 6. If 8 is subtracted from each of the numbers, the ratio becomes 4 : 5. Find the numbers.
4 Indians and 4 Chinese can do a piece of work in 3 days. While 2 Indians and 5 Chinese can finish it in 4 days. How long would it take for 1 Indian to do it? How long would it take for 1 Chinese to do it?
Samacheer Kalvi solutions for Mathematics [English] Class 9 TN Board 3 Algebra Exercise 3.15 [Pages 134 - 136]
Multiple choice questions
If x3 + 6x2 + kx + 6 is exactly divisible by (x + 2), then k = ?
−6
−7
−8
11
The root of the polynomial equation 2x + 3 = 0 is
`1/3`
`-1/3`
`-3/2`
`-2/3`
The type of the polynomial 4 – 3x3 is
constant polynomial
linear polynomial
quadratic polynomial
cubic polynomial
If x51 + 51 is divided by x + 1, then the remainder is
0
1
49
50
The zero of the polynomial 2x + 5 is
`5/2`
`-5/2`
`2/5`
`-2/5`
The sum of the polynomials p(x) = x3 – x2 – 2, q(x) = x2 – 3x + 1
x3 – 3x – 1
x3 + 2x2 – 1
x3 – 2x2 – 3x
x3 – 2x2 + 3x – 1
Degree of the polynomial (y3 – 2)(y3 + 1) is
9
2
3
6
Let the polynomials be
(A) −13q5 + 4q2 + 12q
(B) (x2 + 4)(x2 + 9)
(C) 4q8 – q6 + q2
(D) `– 5/7 y^12 + y^3 + y^5`
Then ascending order of their degree is
A, B, D, C
A, B, C, D
B, C, D, A
B, A, C, D
If p(a) = 0 then (x – a) is a ___________ of p(x)
divisor
quotient
remainder
factor
Zeros of (2 – 3x) is ___________
3
2
`2/3`
`3/2`
Which of the following has x – 1 as a factor?
2x – 1
3x – 3
4x – 3
3x – 4
If x – 3 is a factor of p(x), then the remainder is
3
– 3
p(3)
p(–3)
(x + y)(x2 – xy + y2) is equal to
(x + y)3
(x – y)3
x3 + y3
x3 – y3
(a + b – c)2 is equal to __________
(a – b + c)2
(–a – b + c)2
(a + b + c)2
(a – b – c)2
If (x + 5) and (x – 3) are the factors of ax2 + bx + c, then values of a, b and c are
1, 2, 3
1, 2, 15
1, 2, −15
1, −2, 15
Cubic polynomial may have maximum of ___________ linear factors
1
2
3
4
Degree of the constant polynomial is __________
3
2
1
0
Find the value of m from the equation 2x + 3y = m. If its one solution is x = 2 and y = −2
2
− 2
10
0
Which of the following is a linear equation?
`x + 1/x` = 2
x(x – 1) = 2
3x + 5 = `2/3`
x3 – x = 5
Which of the following is a solution of the equation 2x – y = 6?
(2, 4)
(4, 2)
(3, −1)
(0, 6)
If (2, 3) is a solution of linear equation 2x + 3y = k then, the value of k is
12
6
0
13
Which condition does not satisfy the linear equation ax + by + c = 0
a ≠ 0, b = 0
a = 0, b ≠ 0
a = 0, b = 0, c ≠ 0
a ≠ 0, b ≠ 0
Which of the following is not a linear equation in two variable
ax + by + c = 0
0x + 0y + c = 0
0x + by + c = 0
ax + 0y + c = 0
The value of k for which the pair of linear equations 4x + 6y – 1 = 0 and 2x + ky – 7 = 0 represents parallel lines is
k = 3
k = 2
k = 4
k = − 3
A pair of linear equations has no solution then the graphical representation is
If `"a"_1/"a"_2 ≠ "b"_1/"b"_2` where a1x + b1y + c1 = 0 and a2x + b2y + c2 = 0 then the given pair of linear equation has __________ solution(s)
no solution
two solutions
unique
infinite
If `"a"_1/"a"_2 = "b"_1/"b"_2 ≠ "c"_1/"c"_2` where a1x + b1y + c1 = 0 and a2x + b2y + c2 = 0 then the given pair of linear equation has __________ solution(s)
no solution
two solutions
infinite
unique
G.C.D of any two prime numbers is __________
−1
0
1
2
The G.C.D of x4 – y4 and x2 – y2 is
x4 – y4
x2 – y2
(x + y)2
(x + y)4
Solutions for 3: Algebra
![Samacheer Kalvi solutions for Mathematics [English] Class 9 TN Board chapter 3 - Algebra Samacheer Kalvi solutions for Mathematics [English] Class 9 TN Board chapter 3 - Algebra - Shaalaa.com](/images/mathematics-english-class-9-tn-board_6:5f2b1b2038084cf381bfa42c826a928c.jpg)
Samacheer Kalvi solutions for Mathematics [English] Class 9 TN Board chapter 3 - Algebra
Shaalaa.com has the Tamil Nadu Board of Secondary Education Mathematics Mathematics [English] Class 9 TN Board Tamil Nadu Board of Secondary Education solutions in a manner that help students grasp basic concepts better and faster. The detailed, step-by-step solutions will help you understand the concepts better and clarify any confusion. Samacheer Kalvi solutions for Mathematics Mathematics [English] Class 9 TN Board Tamil Nadu Board of Secondary Education 3 (Algebra) include all questions with answers and detailed explanations. This will clear students' doubts about questions and improve their application skills while preparing for board exams.
Further, we at Shaalaa.com provide such solutions so students can prepare for written exams. Samacheer Kalvi textbook solutions can be a core help for self-study and provide excellent self-help guidance for students.
Concepts covered in Mathematics [English] Class 9 TN Board chapter 3 Algebra are Algebraic Expressions, Polynomials, Polynomials in One Variable, Standard Form of a Polynomial, Degree of Polynomial, Types of Polynomials, Arithmetic of Polynomials, Addition of Polynomials, Subtraction of Polynomials, Multiplication of Two Polynomials, Value of a Polynomial, Roots of a Polynomial Equation, Remainder Theorem, Factor Theorem, Concept of Identity, Expansion of (a + b)2 = a2 + 2ab + b2, Expansion of (a - b)2 = a2 - 2ab + b2, Expansion of (a + b)(a - b) = a2-b2, Expansion of (x + a)(x + b), Expansion of (a + b + c)2, Expansion of (x + a)(x + b)(x + c), Expansion of (a + b)3, Expansion of (a - b)3, Factorisation Using Identities, Factorisation Using Identity a2 + 2ab + b2 = (a + b)2, Factorisation Using Identity a2 - 2ab + b2 = (a - b)2, Factorisation Using Identity a2 - b2 = (a + b)(a - b), Factorisation using Identity a2 + b2 + c2 + 2ab + 2bc + 2ac = (a + b + c)2, Factorisation using Identity a3 + b3 = (a + b)(a2 - ab + b2), Factorisation using Identity a3 - b3 = (a - b)(a2 + ab + b2), Factorisation using Identity a3 + b3 + c3 - 3abc = (a + b + c)(a2 + b2 + c2 - ab - bc - ca), Factorising the Quadratic Polynomial (Trinomial) of the type ax2 + bx + c, a ≠ 0., Division Algorithm for Polynomials, Synthetic Division, Highest Common Factor, General Form of Linear Equation in Two Variables, Graph of a Linear Equation in Two Variables, Comparing the Ratios of Coefficients of a Linear Equation, Graphical Method, Methods of Solving Simultaneous Linear Equations by Substitution, Methods of Solving Simultaneous Linear Equations by Elimination Method, Methods of Solving Simultaneous Linear Equations by Cross Multiplication Method, Consistency and Inconsistency of Linear Equations in Two Variables, Zeroes of a Polynomial, Simultaneous method.
Using Samacheer Kalvi Mathematics [English] Class 9 TN Board solutions Algebra exercise by students is an easy way to prepare for the exams, as they involve solutions arranged chapter-wise and also page-wise. The questions involved in Samacheer Kalvi Solutions are essential questions that can be asked in the final exam. Maximum Tamil Nadu Board of Secondary Education Mathematics [English] Class 9 TN Board students prefer Samacheer Kalvi Textbook Solutions to score more in exams.
Get the free view of Chapter 3, Algebra Mathematics [English] Class 9 TN Board additional questions for Mathematics Mathematics [English] Class 9 TN Board Tamil Nadu Board of Secondary Education, and you can use Shaalaa.com to keep it handy for your exam preparation.