Advertisements
Advertisements
Question
Factorise the following:
(a + b)2 + 9(a + b) + 18
Advertisements
Solution
Let (a + b) = x
x2 + 9x + 18
Product = 18, sum = 9
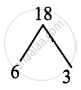
Split the middle term as 6x and 3x
x2 + 9x + 18 = x2 + 6x + 3x + 18
= x(x + 6) + 3(x + 6)
= (x + 6)(x + 3)
But x = a + b
(a + b)2 + 9(a + b) + 18 = (a + b + 6)(a + b + 3)
APPEARS IN
RELATED QUESTIONS
Verify whether the indicated numbers is zeros of the polynomials corresponding to them in the following case:
\[p(x) = x^3 - 6 x^2 + 11x - 6, x = 1, 2, 3\]
f(x) = x3 − 6x2 + 2x − 4, g(x) = 1 − 2x
f(x) = 9x3 − 3x2 + x − 5, g(x) = \[x - \frac{2}{3}\]
Find the remainder when x3 + 3x2 + 3x + 1 is divided by x + 1.
The polynomials ax3 + 3x2 − 3 and 2x3 − 5x + a when divided by (x − 4) leave the remainders R1 and R2 respectively. Find the values of the following case, if R1 + R2 = 0.
Find the value of a such that (x − 4) is a factors of 5x3 − 7x2 − ax − 28.
Find the values of a and b so that (x + 1) and (x − 1) are factors of x4 + ax3 − 3x2 + 2x + b.
If x140 + 2x151 + k is divisible by x + 1, then the value of k is
If x − 3 is a factor of x2 − ax − 15, then a =
Factorise the following:
2a2 + 9a + 10
