Advertisements
Advertisements
Question
Factorise the following:
12x2 + 36x2y + 27y2x2
Solution
3x2[4 + 12y + 9y2]
= 3x2[9y2 + 12y + 4]
Product = 9 × 4 = 36, sum = 12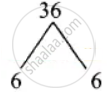
Split the middle term as 6y and 6y
12x2 + 36x2y + 21y2x2 = 3x2[9y2 + 12y + 4]
= 3x2[9y2 + 6y + 6y + 4]
= 3x2[3y(3y + 2) + 2(3y + 2)]
= 3x²(3y + 2)(3y + 2)
= 3x2(3y + 2)2
APPEARS IN
RELATED QUESTIONS
Identify constant, linear, quadratic and cubic polynomials from the following polynomials
`p(x)=2x^2-x+4`
Find the remainder when x3 + 3x2 + 3x + 1 is divided by x.
f(x) = 3x4 + 17x3 + 9x2 − 7x − 10; g(x) = x + 5
f(x) = 2x3 − 9x2 + x + 12, g(x) = 3 − 2x
Find the values of a and b, if x2 − 4 is a factor of ax4 + 2x3 − 3x2 + bx − 4.
x3 − 6x2 + 3x + 10
x3 − 23x2 + 142x − 120
Factorize of the following polynomials:
x3 + 13x2 + 31x − 45 given that x + 9 is a factor
Let f(x) be a polynomial such that \[f\left( - \frac{1}{2} \right)\] = 0, then a factor of f(x) is
Factorise:
2x3 – 3x2 – 17x + 30
