Advertisements
Advertisements
Question
Factorise the following polynomials using synthetic division:
x3 – 3x2 – 10x + 24
Solution
p(x) – x3 – 3x2 – 10x + 24
p(1) = 13 – 3(1)2 – 10(1) + 24
= 1 – 3 – 10 + 24
= 25 – 13
≠ 0
x – 1 is not a factor
p(–1) = (–1)3 – 3(–1)2 – 10(–1) + 24
= – 1 – 3(1) + 10 + 24
= – 1 – 3 + 10 + 24
= 34 – 4
= 30
≠ 0
x + 1 is not a factor
p(2) = 23 – 3(2)2 – 10(2) + 24
= 8 – 3(4) – 20 + 24
= 8 – 12 – 20 + 24
= 32 – 32
= 0
∴ x – 2 is a factor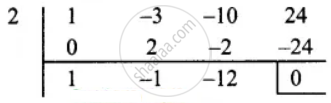
x2 – x – 12 = x2 – 4x + 3x – 12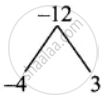
= x(x – 4) + 3(x – 4)
= (x – 4)(x + 3)
∴ The factors of x3 – 3x2 – 10x + 24 = (x – 2)(x – 4)(x + 3)
APPEARS IN
RELATED QUESTIONS
Divide of the following polynomial by synthetic division method and also by linear division method. Write the quotient and the remainder.
`(x^4 + 2x^3 +3x^2 + 4x + 5) ÷ (x + 2)`
Divide the following polynomial by synthetic division method and also by linear division method. Write the quotient and the remainder.
`(x^4 - 3x^2 - 8) ÷ (x + 4)`
Divide the following polynomial by synthetic division method and also by linear division method. Write the quotient and the remainder.
`(y^3 - 3y^2 + 5y - 1) ÷ (y - 1)`
Divide polynomial 3x3 - 8x2 + x + 7 by x - 3 using synthetic method and write the quotient and remainder.
Find the quotient and remainder for the following using synthetic division:
(3x3 – 2x2 + 7x – 5) ÷ (x + 3)
If the quotient obtained on dividing (8x4 – 2x2 + 6x – 7) by (2x + 1) is (4x3 + px2 – qx + 3), then find p, q and also the remainder
Factorise the following polynomials using synthetic division:
2x3 – 3x2 – 3x + 2
Factorise the following polynomials using synthetic division:
x3 + x2 – 14x – 24
Factorise the following polynomials using synthetic division:
x3 – 7x + 6
Factorise the following polynomials using synthetic division:
x3 – 10x2 – x + 10
