Advertisements
Advertisements
Question
Divide of the following polynomial by synthetic division method and also by linear division method. Write the quotient and the remainder.
`(x^4 + 2x^3 +3x^2 + 4x + 5) ÷ (x + 2)`
Solution
Synthetic Division:
Dividend = `x^4 + 2x^3 +3x^2 + 4x + 5`
Divisor = x + 2
Opposite of 2 = −2
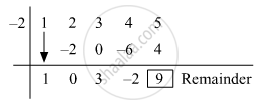
The coefficient form of the quotient is (1, 0, 3, −2).
∴ Quotient = x3 + 3x − 2 and Remainder = 9
Linear Method:
`x^4 + 2x^3 +3x^2 + 4x + 5`
`= x^3 (x + 2) + 3x (x + 2) - 6x + 4x + 5`
`= x^3 (x + 2) + 3x (x + 2) - 2x + 5`
`= x^3 (x + 2) +3x (x + 2) - 2 (x + 2) + 4 + 5`
`= (x + 2) xx (x^3 + 3x - 2) + 9`
APPEARS IN
RELATED QUESTIONS
Divide the following polynomial by synthetic division method and also by linear division method. Write the quotient and the remainder.
`(2m^2 - 3m + 10) ÷ (m - 5)`
Divide the following polynomial by synthetic division method and also by linear division method. Write the quotient and the remainder.
`(2x^4 + 3x^3 + 4x - 2x^2) ÷ (x + 3)`
Divide the following polynomial by synthetic division method and also by linear division method. Write the quotient and the remainder.
`(x^4 - 3x^2 - 8) ÷ (x + 4)`
Divide the following polynomial by synthetic division method and also by linear division method. Write the quotient and the remainder.
`(y^3 - 3y^2 + 5y - 1) ÷ (y - 1)`
Divide polynomial 3x3 - 8x2 + x + 7 by x - 3 using synthetic method and write the quotient and remainder.
Find the quotient and remainder for the following using synthetic division:
(x3 + 2x2 – x – 4) ÷ (x + 2)
If the quotient obtained on dividing (8x4 – 2x2 + 6x – 7) by (2x + 1) is (4x3 + px2 – qx + 3), then find p, q and also the remainder
Factorise the following polynomials using synthetic division:
x3 – 3x2 – 10x + 24
Factorise the following polynomials using synthetic division:
x3 + x2 – 14x – 24
Factorise the following polynomials using synthetic division:
x3 – 7x + 6
