Advertisements
Advertisements
Question
Find the zero of the polynomial in the following:
h(x) = ax + b, a ≠ 0, a, b ∈ R
Solution
h(x) = ax + b, a ≠ 0, a, b ∈ R
= `"a"(x + "b"/"a")`
`"h"(- "b"/"a") = "a"(-"b"/"a") + "b"`
Hence `-"b"/"a"` is the zero of h(x).
APPEARS IN
RELATED QUESTIONS
Verify whether the following zeroes of the polynomial, indicated against them.
p(x) = x2, x = 0
Verify whether the following zeroes of the polynomial, indicated against them.
p(x) = 3x2 – 1, x = `-1/sqrt3,2/sqrt3`
Verify whether the following are zeros of the polynomial, indicated against them, or not
p(x) = x3 – 1, x = 1
Verify whether the following are zeros of the polynomial, indicated against them, or not
p(x) = ax + b, x = `(-"b")/"a"`
Find the number of zeros of the following polynomial represented by their graph
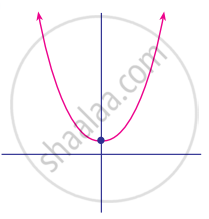
Find the number of zeros of the following polynomial represented by their graph
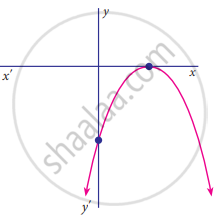
The zero of the polynomial 2x + 5 is
A polynomial cannot have more than one zero
Find p(0), p(1), p(–2) for the following polynomial:
p(y) = (y + 2)(y – 2)
If a, b, c are all non-zero and a + b + c = 0, prove that `a^2/(bc) + b^2/(ca) + c^2/(ab) = 3`.
