Advertisements
Advertisements
प्रश्न
Using a scale of 1 cm to 1 unit for both the axes, draw the graphs of the following equations: 6y = 5x + 10, y = 5x - 15.
From the graph find :
(i) the coordinates of the point where the two lines intersect;
(ii) the area of the triangle between the lines and the x-axis.
उत्तर
6y = 5x + 10
⇒ y = `(5x + 10)/(6)`
The table of 6y = 5x + 10 is
| X | 4 | - 2 | - 8 |
| Y | 5 | 0 | - 5 |
Also, we have
y = 5x - 15
The table of y = 5x - 15 is
| X | 3 | 4 | 5 |
| Y | 0 | 5 | 10 |
Plotting the points in a graph, we get the following graph.
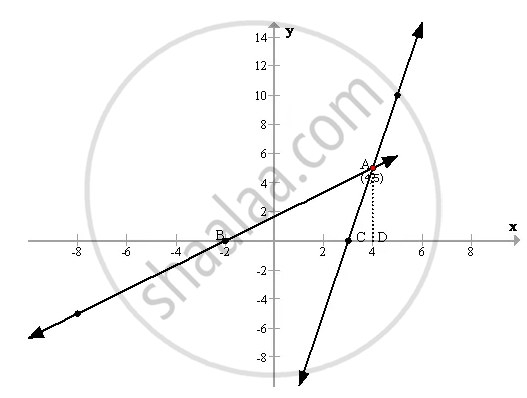
(i)
The two lines intersect at (4, 5)
∴ AD ⊥ BC
AD = 5 units and BC = 5 units
(ii)
The area of the triangles = `(1)/(2) xx "BC" xx "AD"`
= `(1)/(2) xx 5 xx 5`
= `(25)/(2) "sq.units"`
= 12.5 sq.units
APPEARS IN
संबंधित प्रश्न
Plot the points (3, 5) and (− 1, 3) on a graph paper and verify that the straight line passing
through these points also passes through the point (1, 4).
From the choices given below, choose the equation whose graph is given in Fig. below.
(i) y = x (ii) x + y = 0 (iii) y = 2x (iv) 2 + 3y = 7x

[Hint: Clearly, (-1, 1) and (1, -1) satisfy the equation x + y = 0]
Draw the graph of the equation given below. Also, find the coordinates of the point
where the graph cuts the coordinate axes : 6x − 3y = 12
Draw the graph for the equation, given below :
x = 5
Draw the graph for the equation, given below :
3x + 2y = 6
Draw the graph for the equation given below; hence find the co-ordinates of the points where the graph is drawn meets the co-ordinates axes:
`(2x + 15)/(3) = y - 1`
Draw the graph of the equation
4x + 3y + 6 = 0
From the graph, find :
(i) y1, the value of y, when x = 12.
(ii) y2, the value of y, when x = - 6.
The graph of every linear equation in two variables need not be a line.
If the point (3, 4) lies on the graph of 3y = ax + 7, then find the value of a.
The following observed values of x and y are thought to satisfy a linear equation. Write the linear equation:
| x | 6 | – 6 |
| y | –2 | 6 |
Draw the graph using the values of x, y as given in the above table. At what points the graph of the linear equation cuts the y-axis
