Advertisements
Advertisements
प्रश्न
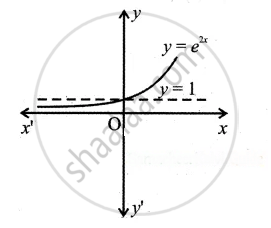
Draw the graph of the following function:
f(x) = e2x
उत्तर
For x = 0, f(x) becomes 1 i.e., the curve cuts the y-axis at y = 1.
For no real value of x, f(x) equals to 0. Thus it does not meet the x-axis for real values of x.
APPEARS IN
संबंधित प्रश्न
Let f be defined by f(x) = x3 – kx2 + 2x, x ∈ R. Find k, if ‘f’ is an odd function.
If f(x) = `x^3 - 1/x^3`, then show that `"f"(x) + "f"(1/x)` = 0
For f(x) = `(x - 1)/(3x + 1)`, write the expressions of `"f"(1/x) and 1/("f"(x))`
If f(x) = ex and g(x) = loge x then find (3f) (1).
Draw the graph of the following function:
f(x) = e-2x
Draw the graph of the following function:
f(x) = `|x|/x`
The graph of y = 2x2 is passing through:
The graph of y = ex intersect the y-axis at:
If f(x) = 2x and g(x) = `1/2^x` then (fg)(x) is:
f(x) = -5, for all x ∈ R is a:
