Advertisements
Advertisements
प्रश्न
Draw the graph of the lines represented by the equations 2x - y = 8 and 4x + 3y = 6 on the same graph. Find the co-ordinates of the point where they intersect.
उत्तर
We have
2x - y = 8
⇒ -y = 8 - 2x
⇒ y = 2x - 8
When
x = -2
⇒ y = -4 - 8
= -12
When
x = 0
⇒ y = -8
When
x = 2
⇒ y = 4 - 8
= -4
| x | -2 | -1 | 0 | 1 | 2 |
| y | -12 | -10 | -8 | -6 | -4 |
Thus ordered pairs of 2x - y = 8 are {(-2, -12), (-1, -10), (0, -8), (1, -6), (2, -4)}.
Also,
4x + 3y = 6
⇒ 3y = 6 - 4x
⇒ y = `(6 - 4x)/(3)`
When x = -2
⇒ y = `(6 + 8)/(3)` = 4.66
When x = 0
⇒ y = `(6)/(3)` = 2
When x = 2
⇒ y = `(6 - 8)/(3)` = -0.66
| x | -2 | -1 | 0 | 1 | 2 |
| y | 4.66 | 3.33 | 2 | 0.66 | -0.66 |
Thus ordered pairs of 4x + 3y = 6 are {(-2, 4.66), (-1, 3.33), (0.2), (1, 0.66), (2, -0.66)}.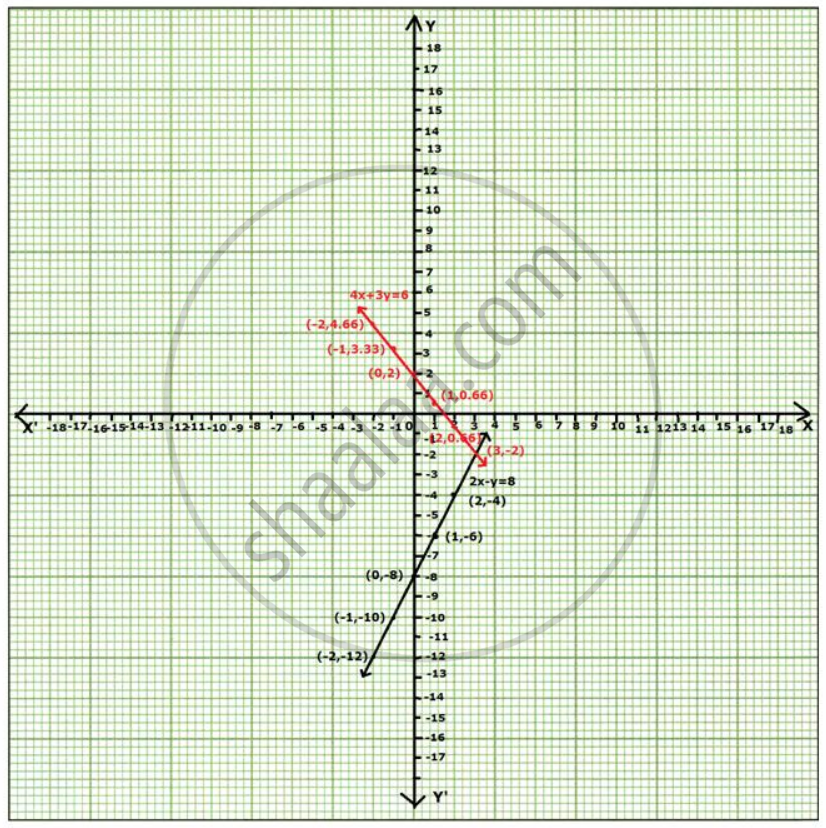
The point of intersection is (3, -2).
APPEARS IN
संबंधित प्रश्न
Draw the graph for the linear equation given below:
x + 3 = 0
Draw the graph for the linear equation given below:
2x - 7 = 0
Draw the graph for the linear equation given below:
5x+ y = 0.
Draw the graph for the linear equation given below:
x + 2y = 0
Draw the graph for the linear equation given below:
`(x - 1)/(3) - (y + 2)/(2) = 0`
Draw the graph for the linear equation given below:
x + 5y + 2 = 0
For the pair of linear equations given below, draw graphs and then state, whether the lines drawn are parallel or perpendicular to each other.
2x - 3y = 6
`x/(2) + y/(3) = 1`
Use the graphical method to show that the straight lines given by the equations x + y = 2, x - 2y = 5 and `x/(3) + y = 0` pass through the same point.
Draw the graph of the lines y = x + 2, y = 2x - 1 and y = 2 from x = -3 to 4, on the same graph paper. Check whether the lines drawn are parallel to each other.
Draw the graph of the lines represented by the equations x + y = 4 and 2x - y = 2 on the same graph. Find the coordinates of the point where they intersect
