Advertisements
Advertisements
Question
Draw the graph of the lines represented by the equations 2x - y = 8 and 4x + 3y = 6 on the same graph. Find the co-ordinates of the point where they intersect.
Solution
We have
2x - y = 8
⇒ -y = 8 - 2x
⇒ y = 2x - 8
When
x = -2
⇒ y = -4 - 8
= -12
When
x = 0
⇒ y = -8
When
x = 2
⇒ y = 4 - 8
= -4
| x | -2 | -1 | 0 | 1 | 2 |
| y | -12 | -10 | -8 | -6 | -4 |
Thus ordered pairs of 2x - y = 8 are {(-2, -12), (-1, -10), (0, -8), (1, -6), (2, -4)}.
Also,
4x + 3y = 6
⇒ 3y = 6 - 4x
⇒ y = `(6 - 4x)/(3)`
When x = -2
⇒ y = `(6 + 8)/(3)` = 4.66
When x = 0
⇒ y = `(6)/(3)` = 2
When x = 2
⇒ y = `(6 - 8)/(3)` = -0.66
| x | -2 | -1 | 0 | 1 | 2 |
| y | 4.66 | 3.33 | 2 | 0.66 | -0.66 |
Thus ordered pairs of 4x + 3y = 6 are {(-2, 4.66), (-1, 3.33), (0.2), (1, 0.66), (2, -0.66)}.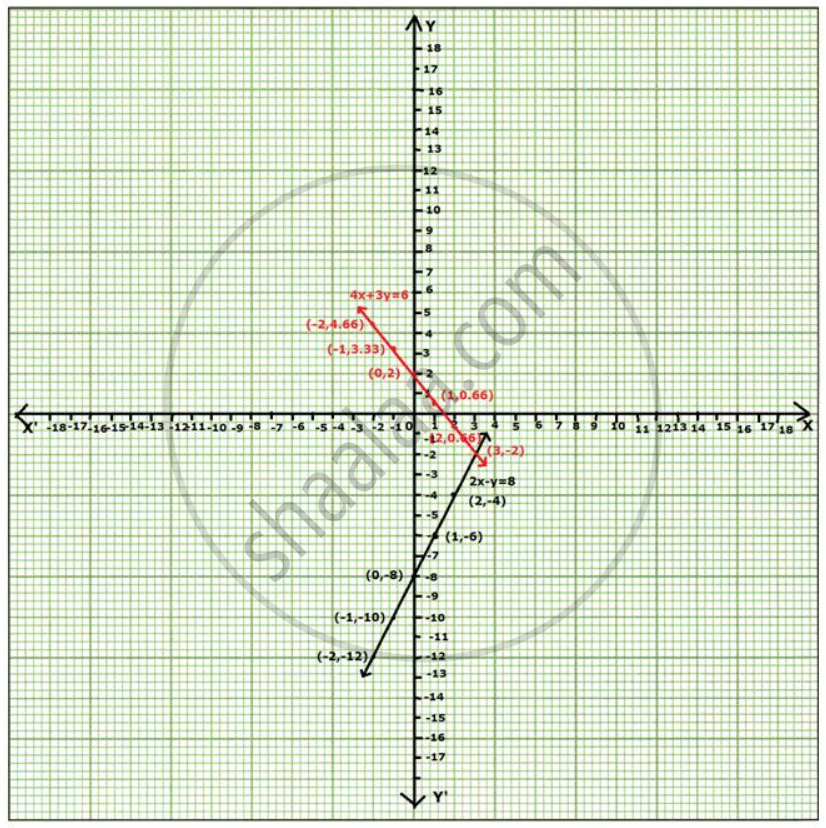
The point of intersection is (3, -2).
APPEARS IN
RELATED QUESTIONS
Draw the graph of the equation given below.
x + y = 2
Draw the graph for the linear equation given below:
y = 3x
Draw the graph for the linear equation given below:
5x+ y = 0.
Draw the graph for the linear equation given below:
y = 2x + 3
Draw the graph for the linear equation given below:
`(x - 1)/(3) - (y + 2)/(2) = 0`
Draw the graph for the equation given below:
`(1)/(2) x + (2)/(3) y = 5`.
On the same graph paper, plot the graphs of y = 2x - 1, y = 2x and y = 2x + 1 from x = - 2 to x = 4. Are the graphs (lines) drawn parallel to each other?
Draw a graph of each of the following equations: 3y + 2x = 11
Draw a graph for each of the following equations and find the coordinates of the points where the line drawn meets the x-axis and y-axis: 2x + 3y = 12
Draw the graph of the lines y = x + 2, y = 2x - 1 and y = 2 from x = -3 to 4, on the same graph paper. Check whether the lines drawn are parallel to each other.
