Advertisements
Advertisements
प्रश्न
दर्शाइए कि मूल बिन्दु से जाने वाली और रेखा y = mx + c से θ कोण बनाने वाली उस रेखा का समीकरण `"y"/"x" = ±("m" + tan θ)/(1 - "m" tan θ)` हैं।
उत्तर
रेखा PA का समीकरण y = mx + c है
यह रेखा OP के साथ कोण θ बनाती है।
रेखा PA की ढाल = m
मान लीजिए OP की ढाल = m1 है।
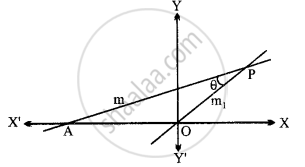
अब tan θ = ± `("m"_1 - "m")/(1 + "m"_1"m")`, जहाँ m = tan θ
+ve चिन्ह लेने पर, tan θ = ± `("m"_1 - "m")/(1 + "m"_1"m")`
या `(1 + "m"_1"m")tan θ = "m"_1 - "m"`
या tan θ + m1 m tan θ = m1 - m
या m + tan θ = m(1 - m tan θ)
या `"m"_1 = ("m" + tan θ)/(1 - "m" tan θ)`
-ve चिन्ह लेने पर,
`"m"_1 = ("m" + tan θ)/(1 - "m" tan θ)`
`(- 1 + "m"_1"m") tan θ = "m"_1 - "m"`
या (1 + m1m) tan θ = −m1 + m
m1(1 + m tan θ) = m − tan θ
∴ `"m"_1 = ("m" - tan θ)/(1 + "m" tan θ)`
इसलिए दोनों ढालों को `("m" ± tan θ)/(1 "m" ± tan θ)` से दर्शाया जाता है।
∴ मूल बिंदु (0, 0) से जाने वाली रेखा का समीकरण,
(y - 0) = m1 (x - 0)
y =m1 × x
या `"y"/"x" = "m"_1`
∴ अभीष्ट रेखाओं का समीकरण
`"y"/"x" = ("m" ± tan θ)/(1 ± tan θ)`
APPEARS IN
संबंधित प्रश्न
रेखा x – 7y + 5 = 0 पर लंब और x-अंत: खंड 3 वाली रेखा का समीकरण ज्ञात कीजिए।
रेखाओं `sqrt3"x" + "y" = 1` और `"x" + sqrt3"y" = 1` के बीच का कोण ज्ञात कीजिए।
बिंदुओं (h, 3) और (4, 1) से जाने वाली रेखा, रेखा 7x – 9y – 19 = 0 को समकोण पर प्रतिच्छेद करती है। h का मान ज्ञात कीजिए।
बिंदु (−1, 3) से रेखा 3x – 4y – 16 = 0 पर डाले गये लंबपाद के निर्देशांक ज्ञात कीजिए।
मूल बिंदु से रेखा y = mx + c पर डाला गया लंब रेखा से बिंदु (−1, 2) पर मिलता है। m और c के मान ज्ञात कीजिए।
यदि p और q क्रमशः मूल बिंदु से रेखाओं x cos θ – y sin θ = k cos 2θ और x sec θ +y cosec θ = k पर लंब की लंबाइयाँ हैं तो सिद्ध कीजिए कि p2 + 4q2 = k2
शीर्षों A(2, 3), B(4, –1) और C(1, 2) वाले त्रिभुज ABC के शीर्ष A से उसकी संमुख भुजा पर लंब डाला गया है। लंब की लंबाई तथा समीकरण ज्ञात कीजिए।
यदि p मूल बिंदु से उस रेखा पर डाले लंब की लंबाई हो जिस पर अक्षों पर कटे अंत: खंड a और b हों, तो दिखाइए कि `1/"p"^2 = 1/"a"^2 + 1/"b"^2`
उन रेखाओं के समीकरण ज्ञात कीजिए जिनके अक्षों से कटे अंतः खंडों का योग और गुणनफल क्रमशः 1 और –6 है।
यदि तीन रेखाएँ जिनके समीकरण y = m1x + c1, y = m2x + c2 और y = m3x + c3 हैं, संगामी हैं तो दिखाइए कि m1(c2 – c3) + m2(c3 – c1) + m3(c1 – c2) = 0
समकोण त्रिभुज के कर्ण के अंतय बिंदु (1, 3) और (−4, 1) हैं। त्रिभुज के पाद (legs) (समकोणीय भुजाओ) का एक समीकरण ज्ञात कीजिए जो कि दोनों अक्षरों के सामांतर हो।
समांतर रखाओं 9x + 6y – 7 = 0 और 3x + 2y + 6 = 0 से समदूरस्थ रेखा का समीकरण ज्ञात कीजिए।
दिखाइए कि `(sqrt("a"^2 - "b"^2), 0)` और `(-sqrt("a"^2 - "b"^2), 0)` बिंदुओं से रेखा `"x"/"a" cos θ + "y"/"b" sin θ = 1` पर खींचे गये लंबों की लंबाइयों का गुणनफल b2 है।
एक व्यक्ति समीकरणों 2x – 3y + 4= 0 और 3x + 4y – 5 = 0 से निरूपित सरल रेखीय पथों के संधि बिंदुओं (junction/crossing) पर खड़ा है और समीकरण 6x – 7y + 8 = 0 से निरूपित पथ पर न्यूनतम समय में पहुँचना चाहता है। उसके द्वारा अनुसरित पथ का समीकरण ज्ञात कीजिए।
