Advertisements
Advertisements
प्रश्न
D.T अभिक्रिया (ड्यूटीरियम-ट्राइटियम संलयन), \[\ce{_{1}^{2}{H} + _{1}^{3}{H} → _{2}^{4}{He} + n}\] पर विचार कीजिए।
(a) नीचे दिए गए आँकड़ों के आधार पर अभिक्रिया में विमुक्त ऊर्जा का मान Mev में ज्ञात कीजिए।
`"m"(""_1^2 "H")` = 2.014102 u
`"m"(""_1^3 "H")` = 3.016049 u
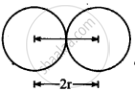
(b) इयूटीरियम एवं ट्राइटियम दोनों की त्रिज्या लगभग 1.5 fm मान लीजिए। इस अभिक्रिया में, दोनों नाभिकों के मध्य कूलॉम प्रतिकर्षण से पार पाने के लिए कितनी गतिज ऊर्जा की आवश्यकता है? अभिक्रिया प्रारम्भ करने के लिए गैसों (0 तथा 1 गैसें) को किस ताप तक ऊष्मित कि या जाना चाहिए?
(संकेत : किसी संलयन क्रिया के लिए आवश्यक गतिज ऊर्जा = संलयन क्रिया में संलग्न कणों की औसत तापीय गतिज ऊर्जा = 2 (3KT/2); K: बोल्ट्ज़मान नियतांक तथा T = परम ताप)
उत्तर
(a) दी गई अभिक्रिया का समीकरण निम्नलिखित है-
\[\ce{_{1}^{2}{H} + _{1}^{3}{H} → _{2}^{4}{He} + _{0}^{1}n + Q}\]
जहाँ Q = `["m"_"N"(""_1^2"H") + "m"_"N"(""_1^3"H") - "m"_"N"(""_2^4"He") - "m"_"n"]"u" xx 931.5 " MeV u"^-1`
`= ["m"(""_1^2"H") - "m"_"e" + "m"(""_1^3"H") - "m"_"e" - "m"(""_2^4"He") + 2"m"_"e" - "m"_"n"] xx 931.5`MeV
= [2.014102 + 3.016049 - 4.002603 - 1.008665] × 931.5
= 0.018883 × 931.5 = 17.59 MeV
(b) ड्यूटीरियम तथा ट्राइटियम प्रत्येक पर आवेश
q1 + q2 = + 1.6 × 10-19 C
प्रत्येक की त्रिज्या r = 1.5 fm = 1.5 × 10-15 m
दोनों के बीच कुलॉम अवरोध
U = निकाय की विद्युत स्थितिज ऊर्जा जबकि दोनों परस्पर संपर्क में हैं।
माना उक्त कूलॉम अवरोध को पार करने के लिए प्रत्येक कण को K गतिज ऊर्जा की आवश्यकता होती है।
तब K + K = U ⇒ 2K = U
अतः कुल गतिज ऊर्जा = `(7.68 xx 10^-14)/(1.6 xx 10^-19)`eV = 480.0 keV
परन्तु कण की तापीय गतिज ऊर्जा K = `3/2`kT
`therefore 3/2 "kT" = 1/2 "U"`
`=> "T" = "U"/"3k"`
अभीष्ट परमताप T = `(7.68 xx 10^-14)/(3 xx 1.38 xx 10^-23) = 1.85 xx 10^9` K
APPEARS IN
संबंधित प्रश्न
माना कि हम \[\ce{_{26}^{56}{Fe}}\] नाभिक के दो समान अवयवों \[\ce{_{13}^{28}{Al}}\] में विखण्डन पर विचार करें।
क्या ऊर्जा की दृष्टि से यह विखण्डन सम्भव है? इस प्रक्रम का Q-मान ज्ञात करके अपना तर्क प्रस्तुत करें।
दिया है : m(\[\ce{_{26}^{56}{Fe}}\]) = 55.93494 u एवं m(\[\ce{_{13}^{28}{Al}}\]) = 27.98191 u.
तीव्र न्यूट्रॉनों द्वारा \[\ce{_{92}^{238}{U}}\] के विखण्डन पर विचार कीजिए। किसी विखण्डन प्रक्रिया में प्राथमिक अंशों (Primary fragments) के बीटा-क्षय के पश्चात कोई न्यूट्रॉन उत्सर्जित नहीं होता तथा \[\ce{_{58}^{140}{P}}\] तथा \[\ce{_{34}^{99}{Ru}}\] अन्तिम उत्पाद प्राप्त होते हैं। विखण्डन प्रक्रिया के लिए के मान का परिकलन कीजिए। आवश्यक आँकड़े इस प्रकार हैं
m(\[\ce{_{92}^{238}{U}}\]) = 238.05079 u
m(\[\ce{_{58}^{140}{Ce}}\]) = 139.90543 u
m(\[\ce{_{34}^{99}{Ru}}\]) = 98.90594 u
सूर्य के अभ्यंतर में (a) 1kg हाइड्रोजन के संलयन के समय विमुक्त ऊर्जा का परिकलन कीजिए। (b) विखण्डन रिएक्टर में 1.0 kg \[^{235}{\text{U}}\] के विखण्डन में विमुक्त ऊर्जा का परिकलेन कीजिए। (c) प्रश्न के खण्ड (a) तथा (b) में विमुक्त ऊर्जाओं की तुलना कीजिए।
