Question

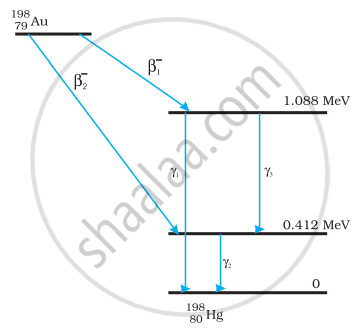
नीचे दी गई क्षय-योजना में, γ-क्षयों की विकिरण आवृत्तियाँ एवं β-कणों की अधिकतम गतिज ऊर्जाएँ ज्ञात कीजिए। दिया है:

m(¹⁹⁸Au) = 197.968233 u

m(¹⁹⁸Hg) =197.966760 u

Answer 1

चित्र से, E₁ = \[\ce{_{80}^{198}{Hg}}\] की निम्नतम ऊर्जा स्तर में ऊर्जा = 0 MeV

E₂ = \[\ce{_{80}^{198}{Hg}}\] की प्रथम उत्तेजित अवस्था में ऊर्जा = 0.412 MeV

E₃ = \[\ce{_{80}^{198}{Hg}}\] की द्वितीय उत्तेजित अवस्था में ऊर्जा = 1.088 MeV

माना उत्सर्जित γ फोटॉनों (γ₁, γ₂ व γ₃) की आवृत्तियाँ क्रमशः ν₁,ν₂ व ν₃ हैं।

तब `"v"_1 = (Delta "E")/"h" = ("E"_3 - "E"_1)/"h" = (1.088 xx 1.6 xx 10^-13
"J" - 0)/(6.62 xx 10^-34)`

= 2.63 × 10²⁰ Hz

`"v"_2 = ("E"_2 - "E"_1)/"h" = (0.412 xx 1.6 xx 10^-13 "J" - 0)/(6.62 xx 10^-34)`

= 9.96 × 10¹⁹ Hz

`"v"_3 = ("E"_3 - "E"_2)/"h" = ((1.088 - 0.412) xx 1.6 xx 10^-13 "J")/(6.62 xx 10^-34)`

= 1.63 × 10²⁰ Hz

जबकि इन फोटॉनों की ऊर्जाएँ निम्नलिखित हैं

E (γ₁) = E₃ – E₁ = 1.088 MeV

E (γ₂)= E₂– E₁ = 0.412 Mev

E (γ₃) = E₃ – E₂ = 1.088- 0.412 = 0.676 MeV

\[\ce{_{79}^{198}{Au}}\] के β^–₁-क्षय में Au नाभिक पहले एक β कण उत्सर्जित करता है तत्पश्चात् γ₁-फोटॉन को । उत्सर्जित करके \[\ce{_{80}^{198}{Hg}}\] नाभिक में बदल जाता है; अतः 
\[\ce{_{79}^{198}{Au}}\] के β^–₁-क्षय का समीकरण निम्नलिखित है।

\[\ce{_79^198Au -> _80^198Hg + _(-1)^0e + E(\beta_1^-) + E(\gamma_1)}\]

यहाँ E(β^–₁) तथा E (γ₁) इन कणों की ऊर्जाएँ हैं। स्पष्ट है कि E(β^–₁) का मान अधिकतम होगा यदि \[\ce{_{80}^{198}{Hg}}\] की गतिज ऊर्जा शून्य हो। अर्थात् अभिक्रिया की सम्पूर्ण ऊर्जा केवल β-कण तथा γ-कोटॉन की ऊर्जा के रूप में निकलें।

∴ β -कण की महत्तम गतिज ऊर्जा

`"E"(beta_1^-) = "Q" - "E"(gamma_1)`

`= ["m"_"N" (""_79^198"Au") - "m"_"N"(""_80^198"Hg") - "m"_"e"] xx 931.5 " MeV" - "E"(gamma_1)`

`= ["m"(""_79^198"Au") - 79"m"_"e" - "m"(""_80^198"Hg") + 80 "m"_"e" - "m"_"e"] xx 931.5 - "E"(gamma_1)`

`= ["m" (""_79^198"Au") - "m" (""_80^198"Hg")] xx 931.5 - "E"(gamma_1)`

= [197.968233 - 197.966760] × 931.5 - 1.088

= 0.001473 × 931.5 - 1.088

= (1.372 - 1.088) MeV = 0.284 MeV

\[\ce{_{79}^{198}{Au}}\] के β^–₂क्षय में Au नांभिक पहले β-कण उत्सर्जित करता है तत्पश्चात् γ₂ फोटॉन उत्सर्जित करता हुआ \[\ce{_{80}^{198}{Hg}}\] नाभिक में बदल जाता है।

इसे क्षय का समक्रण निम्नलिखित है

\[\ce{_79^198Au -> _80^198Hg + _(-1)^0e + E(\beta_2^-) + E(\gamma_2)}\]

∴ उत्सर्जित \[\ce{\beta_2^-}\] कण की महत्तम गतिज ऊर्जा

`"E"(beta_2^-) = "Q" - "E"(gamma_2)`

`= ["m")"N"(""_79^198 "Au") - "m"_"N" (""_80^198 "Hg") + 80 "m"_"e" - "m"_"e"] xx 931.5 - "E"(gamma_2)`

`= ["m"(""_79^198 "Au") - 79 "m"_"e" - "m"(""_80^198 "Hg") + 80"m"_"e" - "m"_"e"] xx 931.5 - "E"(gamma_2)`

`= ["m"(""_79^198 "Au") - "m"(""_80^198 "Hg")] xx 931.5 - "E"(gamma_2)`

= [197.968233 - 197.966760] × 931.5 - 0.412

= 1.372 - 0.676

= 0.960 MeV