Advertisements
Advertisements
प्रश्न
एक आयताकार बाग, जिसकी लंबाई, चौड़ाई से 4 m अधिक है, का अर्धपरिमाप 36 m है। बाग की विमाएँ ज्ञात कीजिए।
उत्तर
मान लीजिए बगीचे की चौड़ाई x और लंबाई y है।
प्रश्न के अनुसार
y - x = 4
y + x = 36
y - x = 4
y = x + 4
| x | 0 | 8 | 12 |
| y | 4 | 12 | 16 |
y + x = 36
| x | 0 | 36 | 16 |
| y | 36 | 0 | 20 |
अतः, ग्राफिक निरूपण इस प्रकार है:
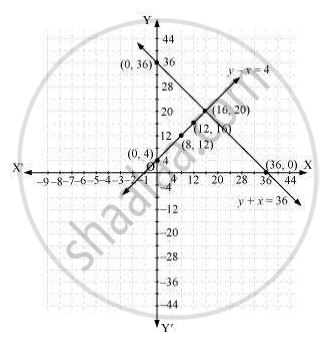
आकृति से यह देखा जा सकता है कि ये रेखाएँ एक दूसरे को केवल बिंदु (16, 20) पर प्रतिच्छेद कर रही हैं। इसलिए, दिए गए बगीचे की लंबाई और चौड़ाई क्रमशः 20 मीटर और 16 है।
APPEARS IN
संबंधित प्रश्न
2 kg सेब और 1 kg अंगूर का मूल्य किसी दिन ₹ 160 था। एक महीने बाद 4 kg सेब और दो kg अंगूर का मूल्य ₹ 300 हो जाता है। इस स्थिति को बीजगणितीय तथा ज्यामितीय रूपों में व्यक्त कीजिए।
अनुपातों `bb(a_1/a_2, b_1/b_2)` और `bb(c_1/c_2)` की तुलना कर ज्ञात कीजिए कि निम्न रैखिक समीकरण के युग्म संगत हैं या असंगत:
5x - 3y = 11; -10x + 6y = -22
अनुपातों `bb(a_1/a_2, b_1/b_2)` और `bb(c_1/c_2)` की तुलना कर ज्ञात कीजिए कि निम्न रैखिक समीकरण के युग्म संगत हैं या असंगत:
`4/3x + 2y = 8`; 2x + 3y = 12
एक रैखिक समीकरण 2x + 3y - 8 = 0 दी गई है। दो चरों में एक ऐसी और रैखिक समीकरण लिखिए ताकि प्राप्त युग्म का ज्यामितीय निरूपण जैसा कि
- प्रतिच्छेद करती रेखाएँ हों।
- समांतर रेखाएँ हों।
- संपाती रेखाएँ हों।
क्या समीकरणों के निम्नलिखित युग्म का कोई हल नहीं है? अपने उत्तर का औचित्य दीजिए।
`3x + y - 3 = 0, 2x + 2/3y` = 2
क्या रैखिक समीकरणों के निम्नलिखित युग्म संगत हैं? अपने उत्तरों का औचित्य दीजिए।
2ax + by = a, 4ax + 2by – 2a = 0; a, b ≠ 0
समीकरण λx + 3y = –7, 2x + 6y = 14 के युग्म के अपरिमित रूप से अनेक हल होने के लिए, λ का मान 1 होना चाहिए। क्या यह कथन सत्य है? कारण दीजिए।
c के सभी वास्तविक मानों के लिए समीकरण-युग्म x – 2y = 8, 5x – 10y = c का एक अद्वितीय हल हैऔचित्य के साथ उत्तर दीजिए कि यह सत्य है या असत्य।
x = 7 द्वारा निरूपित रेखा x अक्ष के समांतर है औचित्य के साथ उत्तर दीजिए कि यह सत्य है या असत्य।
k के किस (किन) मान (मानों) के लिए, समीकरण-युग्म
kx + 3y = k – 3
12x + ky = k
का कोई हल नहीं होगा ?
