Advertisements
Advertisements
प्रश्न
एक A.P. में, a = 2, d = 8 और Sn = 90 दिया है। n और an ज्ञात कीजिए।
उत्तर
दिया गया है कि a = 2, d = 8, और Sn = 90
`"जैसा कि" S_n = n/2 [2a + (n - 1)d]`
`90 = n/2 [2xx2 + (n - 1)8]`
90 × 2 = 4n + n(11 - 1) × 8
180 = 4n + 8n2 - 8n
180 = 8n2 - 4n
45 = 2n2 - n
2n2 - n - 45 = 0
2n2 - 10n + 9n - 45 = 0
2n (n - 5) + 9(n - 5) = 0
(2n + 9) (n - 5) = 0
∴ या तो 2n + 9 = 0
n = `-9/2`
या n - 5 = 0
n = 5
लेकिन n = `9/2` संभव नहीं है।
∴ n = 5
अब, an = a + (n - 1)d
a5 = 2 + (5 -1) × 8
a5 = 2 + 32
a5 = 34
इस प्रकार, n = 3 और a5 = 34
APPEARS IN
संबंधित प्रश्न
एक A.P. में, a = 3, n = 8 और S = 192 दिया है। d ज्ञात कीजिए।
केंद्र A से प्रारंभ करते हुए, बारी-बारी से केंद्रों A और B को लेते हुए, त्रिज्याओं 0.5 cm, 1.0 cm, 1.5 cm, 2.0 cm,……. वाले उतरोत्तर अर्धवृत्तों को खींचकर एक सर्पिल (Spiral) बनाया गया है, जैसाकि आकृति में दर्शाया गया है। तेरह क्रमागत अर्धवृत्तों से बने इस सर्पिल की कुल लंबाई क्या है? (π = `22/7` लीजिए।)
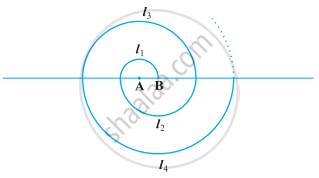
[संकेत: क्रमशः केंद्रों A, B, A, B,... वाले अर्धवृत्तों की लंबाइयाँ l1, l2, l3, l4 हैं।]
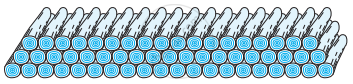
200 लट्ठों (logs) को ढेरी के रूप में इस प्रकार रखा जाता है : सबसे नीचे वाली पंक्ति में 20 लट्ठे, उससे अगली पंक्ति में 19 लट्ठे, उससे अगली पंक्ति में 18 लट्ठे, इत्यादि (देखिए आकृति)। ये 200 लठ्ठे कितनी पंक्तियों में रखे गए हैं तथा सबसे ऊपरी पंक्ति में कितने लट्ठे हैं?
किसी AP में, यदि a = 1, an = 20 और Sn = 399 हों, तो n बराबर ______ है।
ज्ञात कीजिए कि 55 एक AP : 7, 10, 13,... का पद है या नहीं। यदि हाँ, तो ज्ञात कीजिए कि यह कौन-सा पद है।
AP: `- 4/3, -1, -2/3,..., 4 1/3` के दोनों मध्य पदों का योग ज्ञात कीजिए।
योग ज्ञात कीजिए :
`(a - b)/(a + b) + (3a - 2b)/(a + b) + (5a - 3b)/(a + b) + ...` 11 पदों तक
यदि an = 3 – 4n हो, तो दर्शाइए कि a1, a2, a3,... एक AP बनाते हैं। S20 भी ज्ञात कीजिए।
AP: 8, 10, 12,..., 126 के अंतिम 10 पदों का योग ज्ञात कीजिए।
किसी AP में 37 पद हैं। बीचो-बीच के तीन पदों का योग 225 है तथा अंतिम तीन पदों का योग 429 है। वह AP ज्ञात कीजिए।
