Advertisements
Advertisements
प्रश्न
एक बहुफलकी में 20 फलक और 12 शीर्ष हैं। इसके किनारों की संख्या ज्ञात कीजिए।
उत्तर
बहुफलक के लिए ऑयलर के सूत्र का उपयोग करने पर,
F + V – E = 2 ...[जहाँ, F = फलक, V = शीर्ष, E = किनारा]
दिया गया है, फलक (F) = 20, शीर्ष (V) = 12
⇒ 20 + 12 – E = 2
⇒ 32 – E = 2
⇒ E = 32 – 2
⇒ E = 30
अतः, बहुफलक के किनारे 30 हैं।
APPEARS IN
संबंधित प्रश्न
क्या ऐसा बहुफलक संभव है जिसके फलकों की संख्या कोई भी संख्या हो? (संकेत: एक पिरामिड के बारे में सोचिये।)
एक बहुफलकी में, यदि F = V = 5 है, तो इस आकार में किनारों की संख्या होगी -
निम्न में से कौन एक बहुफलकी के लिए सत्य नहीं हो सकता?
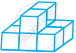में घनों की संख्या ______ है।
यदि एक बहुफलकी में शीर्षो और फलकों की संख्याओं का योग 14 है, तो इस आकार में किनारों की संख्या ______ है।
निम्न आकारों को देखिए और बताइए कि इनमें कौन-कौन बहुफलकी हैं।
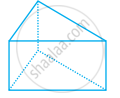
निम्न आकारों को देखिए और बताइए कि इनमें कौन-कौन बहुफलकी हैं।
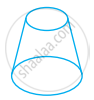
निम्न आकारों को देखिए और बताइए कि इनमें कौन-कौन बहुफलकी हैं।
क्या किसी बहुफलकी में V = F = 9 और E = 16 हो सकता है? यदि हाँ, तो इसकी आकृति खींचिए।
जाँच कीजिए कि क्या एक बहुफलकी में V = 12, E = 6 और F = 8 हो सकता है।
