Advertisements
Advertisements
प्रश्न
एक त्रिभुज और एक समांतर चतुर्भुज का एक ही आधार है और क्षेत्रफल भी एक ही है। यदि त्रिभुज की भुजाएँ 26 सेमी, 28 सेमी और 30 सेमी हैं तथा समांतर चतुर्भुज 28 सेमी के आधार पर स्थित है, तो उसकी संगत ऊँचाई ज्ञात कीजिए।
उत्तर
त्रिभुज की भुजाएँ 26 सेमी, 28 सेमी और 30 सेमी हैं।
∴ त्रिभुज का परिमाप (2s) = (26 + 28 + 30) सेमी
⇒ 2s = 84 सेमी
⇒ अर्ध-परिमाप
⇒ S = 42 सेमी
हीरोन के सूत्र का प्रयोग करने पर;
त्रिभुज का क्षेत्रफल
`"त्रिभुज का क्षेत्रफल"=sqrt(s(s-a)(s-b)(s-c))`
`"त्रिभुज का क्षेत्रफल"=[sqrt(42(42-26)(42-28)(42-30))]cm^2`
`=[sqrt(42(16)(14)(12))]cm^2`
= 2 X 2 X 2 X 2 X 3 X 7 सेमी2
= 336 सेमी2
दिया है कि समांतर चतुर्भुज का क्षेत्रफल = त्रिभुज का क्षेत्रफल
⇒ आधार X संगत ऊँचाई = 336 सेमी2
⇒ 28 सेमी X ऊँचाई = 336 सेमी2
⇒ ऊँचाई = 12 सेमी
अतः, समांतर चतुर्भुज की संगत ऊँचाई 12 सेमी है।
APPEARS IN
संबंधित प्रश्न
एक पार्क चतुर्भुज ABCD के आकार का है, जिसमें ∠C = 90° है, AB = 9 मी, BC = 12 मी, CD = 5 मी और AD = 8 मी है। इस पार्क का क्षेत्रफल कितना है?
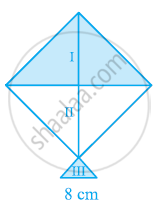
एक पतंग तीन भिन्न-भिन्न रंगों के कागज़ों से बनी है। इन्हें आकृति में I, II और III से दर्शाया गया है। पतंग का ऊपरी भाग 32 सेमी विकर्ण का एक वर्ग है और निचला भाग 6 सेमी, 6 सेमी और 8 सेमी भुजाओं का एक समद्विबाहु त्रिभुज है। ज्ञात कीजिए कि प्रत्येक रंग का कितना कागज़ प्रयुक्त किया गया है।
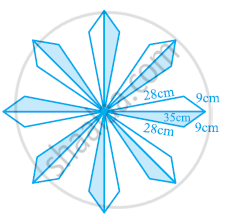
फर्श पर एक फूलों का डिज़ाइन 16 त्रिभुजाकार टाइलों से बनाया गया है, जिनमें से प्रत्येक की भुजाएँ 9 सेमी, 28 सेमी और 35 सेमी हैं (देखिए आकृति )। इन टाइलों को 50 पैसे प्रति सेमी की दर से पालिश कराने का व्यय ज्ञात कीजिए।
एक खेत समलंब के आकार का है जिसकी समांतर भुजाएँ 25 मी और 10 मी हैं। इसकी असमांतर भुजाएँ 14 मी और 13 मी हैं। इस खेत का क्षेत्रफल ज्ञात कीजिए।
एक समद्विबाहु त्रिभुज का क्षेत्रफल `5/4 sqrt(11)` cm2 होगा, यदि उसका परिमाप 11 cm है और आधार 5 cm है।
एक खेत एक समांतर चतुर्भुज के आकार का है, जिसकी भुजाएँ 60 m और 40 m हैं तथा एक विकर्ण 80 m है। इस खेत का क्षेत्रफल ज्ञात कीजिए।
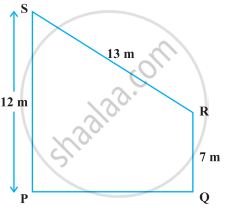
निम्नलिखित आकृति में दी हुई ऊँचाई PQ वाले समलंब PORS का क्षेत्रफल ज्ञात कीजिए।
एक मकान का निर्माण करने के लिए एक आयताकार भूखंड दिया गया, जिसकी लंबाई 40 m है तथा सामने की चौडाई 15 m है। नियमों के अनुसार, सामने और पीछे की ओर न्यूनतम 3 m चौड़ी जगह तथा प्रत्येक अन्य ओर पर न्यूनतम 2 m चौड़ी जगह छोड़नी आवश्यक है। वह अधिकतम क्षेत्र ज्ञात कीजिए जिसमें मकान का निर्माण किया जा सकता है।
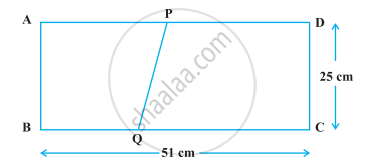
एक आयत ABCD की विमाएँ 51 cm × 25 cm हैं। इस आयत में से एक समलंब PQCD काटा जाता है, जिसकी समांतर भुजाएँ QC और PD हैं और ये 9 : 8 के अनुपात में हैं, जैसा कि निम्नलिखित आकृति में दर्शाया गया है। यदि समलंब PQCD का क्षेत्रफल आयत के क्षेत्रफल का `5/6` भाग है, तो QC और PD की लंबाइयाँ ज्ञात कीजिए।
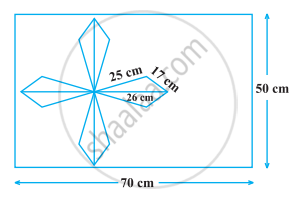
50 cm × 70 cm विमाओं वाली एक आयताकार टाइल पर, निम्नलिखित आकृति में दर्शाए अनुसार एक डिज़ाइन बनाया जाता है। इस डिज़ाइन में 8 त्रिभुज हैं, जिनमें से प्रत्येक की भुजा 26 cm, 17 cm और 25 cm की हैं। डिज़ाइन का पूर्ण क्षेत्रफल ज्ञात कीजिए तथा टाइल के शेष भाग का क्षेत्रफल भी ज्ञात कीजिए।