Advertisements
Advertisements
प्रश्न
एक त्रिभुज की भुजाएँ 35 cm, 54 cm और 61 cm की हैं। इसके सबसे लंबे शीर्षलंब की लंबाई है
विकल्प
`16sqrt(5)` cm
`10sqrt(5)` cm
`24sqrt(5)` cm
28 cm
उत्तर
`bb(24sqrt(5) cm`
स्पष्टीकरण -
दिया गया है - एक त्रिभुज की भुजाएँ क्रमश : a = 35 सेमी, b = 54 सेमी और c = 61 सेमी हैं।
तो, एक त्रिभुज की अर्ध-परिधि है -
`s = (a + b + c)/2`
= `(35 + 54 + 61)/2`
= `150/2`
= 75
त्रिभुज का क्षेत्रफल = `sqrt(s(s - a)(s - b)(s - c))`
= `sqrt(75(75 - 35)(75 - 54)(75 - 61))`
= `sqrt(75 xx 40 xx 21 xx 14)`
= `sqrt(5 xx 5 xx 3 xx 2 xx 2 xx 2 xx 5 xx 3 xx 7 xx 7 xx 2)`
= `5 xx 3 xx 2 xx 2 xx 7sqrt(5)`
= `420sqrt(5)`
जैसा कि आप जानते हैं,
त्रिभुज ABC का क्षेत्रफल = `1/2` × आधार × ऊँचाई
`1/2` × 35 × ऊँचाई = `420sqrt(5)`
ऊँचाई = `(420sqrt(5) xx 2)/35`
ऊँचाई = `24sqrt(5)`
इसलिए, ऊंचाई की लंबाई `24sqrt(5)` है।
APPEARS IN
संबंधित प्रश्न
किसी फ्लाईओवर (Flyover) की त्रिभुजाकार दीवार को विज्ञापनों के लिए प्रयोग किया जाता है। दीवार की भुजाओं की लंबाइयाँ 122 m, 22 m और 120 m हैं (देखिए आकृति)। इस विज्ञापन से प्रति वर्ष ₹ 5000 प्रति m2 की प्राप्ति होती है। एक कंपनी ने एक दीवार को विज्ञापन देने के लिए 3 महीने के लिए किराए पर लिया। उसने कुल कितना किराया दिया?
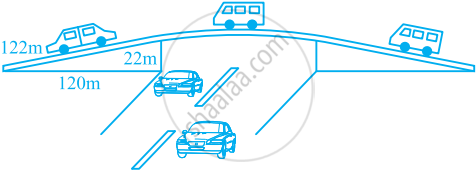
किसी पार्क में एक फिसल पट्टी (Slide) बनी हुई है। इसकी पार्श्वीय दीवारों (Side Walls) में से एक दीवार पर किसी रंग से पेंट किया गया है और उस पर ‘‘पार्क को हरा-भरा और साफ़ रखिए” लिखा हुआ है। (देखिए आकृति)। यदि इस दीवार की विमाएँ 15 m, 11 m और 6 m हैं, तो रंग से पेंट हुए भाग का क्षेत्रफल ज्ञात कीजिए।
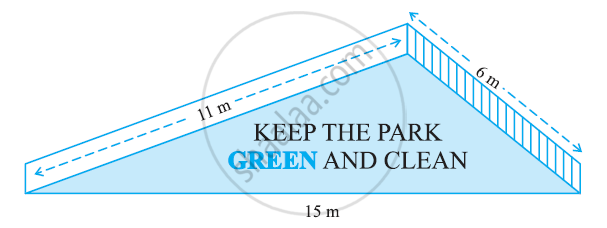
एक त्रिभुज की भुजाओं का अनुपात 12 : 17 : 25 है और उसका परिमाप 540 cm है। इस त्रिभुज का क्षेत्रफल ज्ञात कीजिए।
`2sqrt(3)` cm भुजा वाले समबाहु त्रिभुज का क्षेत्रफल है
आधार 2 cm और बराबर भुजाओं में से एक भुजा 4 cm वाले समद्विबाहु त्रिभुज का क्षेत्रफल है
एक समबाहु त्रिभुज का क्षेत्रफल `20sqrt(3)` cm2 है, जिसकी प्रत्येक भुजा 8 cm है।
एक त्रिभुजाकार मैदान जिसकी भुजाएँ 51 m, 37 m और 20 m हैं को 3 रु. प्रति m2 की दर से समतल कराने का व्यय 918 रु है।
भुजाओं 50 m, 65 m और 65 m वाले त्रिभुजाकार खेत में 7 रु. प्रति m2 की दर से घास लगवाने का व्यय ज्ञात कीजिए।
एक समबाहु त्रिभुज के अभ्यंतर में स्थित किसी बिंदु से तीनों भुजाओं पर लंब डाले जाते हैं। इन लंबों की लंबाई 14 cm, 10 cm और 6 cm हैं। इस त्रिभुज का क्षेत्रफल ज्ञात कीजिए।
एक त्रिभुजाकार खेत का परिमाप 420 m है तथा इसकी भुजाओं का अनुपात 6 : 7 : 8 है। इस खेत का क्षेत्रफल ज्ञात कीजिए।
