Advertisements
Advertisements
प्रश्न
एक त्रिभुज की भुजाओं का अनुपात 12 : 17 : 25 है और उसका परिमाप 540 cm है। इस त्रिभुज का क्षेत्रफल ज्ञात कीजिए।
उत्तर
मान लीजिए दिए गए त्रिभुज की भुजाओं के बीच का सामान्य अनुपात x है।
इसलिए, त्रिभुज की भुजाएँ 12x, 17x और 25x होंगी।
त्रिभुज का परिमाप = 540 cm
12x + 17x + 25x = 540 cm
54x = 540 cm
x = 10 cm
त्रिभुज की भुजाएँ 120 cm, 170 cm और 250 cm होंगी।
s = `"त्रिभुज का परिमाप"/2`
= `540/2`
= 270 cm
हेरोन के सूत्र द्वारा,
त्रिभुज का क्षेत्रफल = `sqrt(s(s-a)(s-b)(s-c))`
= `[sqrt(270(270-120)(270-170)(270-250))]cm^2`
= `[sqrt(270xx150xx100xx20)]cm^2`
= `sqrt(10^2 xx 10^2 xx 3^2 xx 3^2 xx 5^2 xx 2^2) cm^2`
= (10 × 10 × 3 × 3 × 5 × 2) cm2
= 9,000 cm2
अतः इस त्रिभुज का क्षेत्रफल 9,000 cm2 है।
APPEARS IN
संबंधित प्रश्न
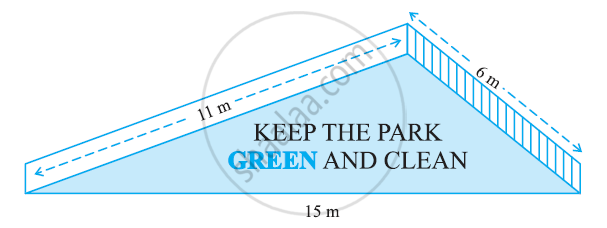
किसी पार्क में एक फिसल पट्टी (Slide) बनी हुई है। इसकी पार्श्वीय दीवारों (Side Walls) में से एक दीवार पर किसी रंग से पेंट किया गया है और उस पर ‘‘पार्क को हरा-भरा और साफ़ रखिए” लिखा हुआ है। (देखिए आकृति)। यदि इस दीवार की विमाएँ 15 m, 11 m और 6 m हैं, तो रंग से पेंट हुए भाग का क्षेत्रफल ज्ञात कीजिए।
`2sqrt(3)` cm भुजा वाले समबाहु त्रिभुज का क्षेत्रफल है
आधार 2 cm और बराबर भुजाओं में से एक भुजा 4 cm वाले समद्विबाहु त्रिभुज का क्षेत्रफल है
एक त्रिभुज ABC का क्षेत्रफल 8 cm2 है, जिसमें AB = AC = 4 cm है तथा ∠A = 90° है।
एक समबाहु त्रिभुज का क्षेत्रफल `20sqrt(3)` cm2 है, जिसकी प्रत्येक भुजा 8 cm है।
यदि एक समचतुर्भुज की एक भुजा 10 cm और एक विकर्ण 16 cm है, तो उस समचतुर्भुज का क्षेत्रफल 96 cm2 है।
एक समबाहु त्रिभुज के अभ्यंतर में स्थित किसी बिंदु से तीनों भुजाओं पर लंब डाले जाते हैं। इन लंबों की लंबाई 14 cm, 10 cm और 6 cm हैं। इस त्रिभुज का क्षेत्रफल ज्ञात कीजिए।
एक समद्विबाहु त्रिभुज का परिमाप 32 cm है। एक बराबर भुजा और आधार का अनुपात 3 : 2 है। इस त्रिभुज का क्षेत्रफल ज्ञात कीजिए।
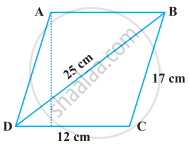
आकृति में दिए हुए समांतर चतुर्भुज का क्षेत्रफल ज्ञात कीजिए। साथ ही, शीर्ष A से भुजा DC पर शीर्षलंब की लंबाई ज्ञात कीजिए।
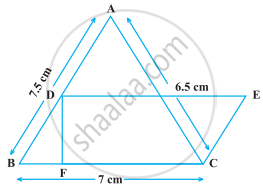
निम्नलिखित आकृति में, ∆ABC की भुजाओं में AB = 7.5 cm, AC = 6.5 cm और BC = 7 cm है। आधार BC पर एक समांतर चतुर्भुज DBCE की रचना की जाती है, जो क्षेत्रफल में ∆ABC के बराबर है। इस समांतर चतुर्भुज की ऊँचाई DF ज्ञात कीजिए।