Advertisements
Advertisements
प्रश्न
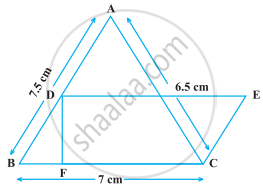
निम्नलिखित आकृति में, ∆ABC की भुजाओं में AB = 7.5 cm, AC = 6.5 cm और BC = 7 cm है। आधार BC पर एक समांतर चतुर्भुज DBCE की रचना की जाती है, जो क्षेत्रफल में ∆ABC के बराबर है। इस समांतर चतुर्भुज की ऊँचाई DF ज्ञात कीजिए।
उत्तर
अब, पहले ∆ABC का क्षेत्रफल ज्ञात कीजिए।
एक त्रिभुज की भुजाएँ AB = a = 7.5 cm, BC = b = 7 cm और CA = c = 6.5 cm हैं।
अब, त्रिभुज की अर्ध-परिधि,
`s = (a + b + c)/2`
= `(7.5 + 7 + 6.5)/2`
= `21/2`
= 10.5 cm
∴ ΔABC का क्षेत्रफल = `sqrt(s(s - a)(s - b)(s - c))` ...[हीरोन के सूत्र द्वारा]
= `sqrt(10.5(10.5 - 7.5)(10.5 - 7)(10.5 - 6.5))`
= `sqrt(10.5 xx 3 xx 3.5 xx 4)`
= `sqrt(441)`
= 21 cm2 ...(i)
अब, समांतर चतुर्भुज BCED का क्षेत्रफल = आधार × ऊँचाई
= BC × DF
= 7 × DF ...(ii)
प्रश्न के अनुसार,
∆ABC का क्षेत्रफल = समांतर चतुर्भुज BCED का क्षेत्रफल
⇒ 21 = 7 × DF ...[समीकरण (i) और (ii) से]
⇒ DF = `21/4` = 3 cm
अतः, समांतर चतुर्भुज की ऊँचाई 3 cm है।
APPEARS IN
संबंधित प्रश्न
एक त्रिभुज की भुजाओं का अनुपात 12 : 17 : 25 है और उसका परिमाप 540 cm है। इस त्रिभुज का क्षेत्रफल ज्ञात कीजिए।
यदि एक समबाहु त्रिभुज का क्षेत्रफल `16sqrt(3)` cm2 है, तो इस त्रिभुज का परिमाप है
एक त्रिभुज की भुजाएँ 35 cm, 54 cm और 61 cm की हैं। इसके सबसे लंबे शीर्षलंब की लंबाई है
एक समबाहु त्रिभुज का क्षेत्रफल `20sqrt(3)` cm2 है, जिसकी प्रत्येक भुजा 8 cm है।
यदि एक समचतुर्भुज की एक भुजा 10 cm और एक विकर्ण 16 cm है, तो उस समचतुर्भुज का क्षेत्रफल 96 cm2 है।
एक त्रिभुजाकार मैदान जिसकी भुजाएँ 51 m, 37 m और 20 m हैं को 3 रु. प्रति m2 की दर से समतल कराने का व्यय 918 रु है।
भुजाओं 50 m, 65 m और 65 m वाले त्रिभुजाकार खेत में 7 रु. प्रति m2 की दर से घास लगवाने का व्यय ज्ञात कीजिए।
एक समद्विबाहु त्रिभुज का परिमाप 32 cm है। एक बराबर भुजा और आधार का अनुपात 3 : 2 है। इस त्रिभुज का क्षेत्रफल ज्ञात कीजिए।
एक त्रिभुजाकार खेत का परिमाप 420 m है तथा इसकी भुजाओं का अनुपात 6 : 7 : 8 है। इस खेत का क्षेत्रफल ज्ञात कीजिए।
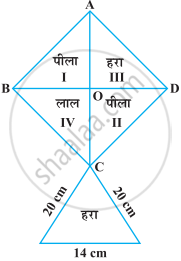
निम्नलिखित आकृति में दी हुई पतंग को बनाने के लिए प्रत्येक शेड (रंग) के कितने कागज की आवश्यकता होगी, यदि ABCD विकर्ण 44 cm वाला एक वर्ग है।