Advertisements
Advertisements
प्रश्न
Explain the variation of g with depth from the Earth’s surface.
उत्तर
Consider a particle of mass m which is in a deep mine on the Earth. (Example: coal mines in Neyveli). Assume the depth of the mine as d. To calculate g’ at a depth d, consider the following points.
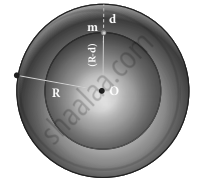
Particle in a mine
The part of the Earth which is above the radius (Re – d) does not contribute to the acceleration. The result is proved earlier and is given as
g’ = `"GM’"/(("R"_"e" - "d")^2)`
Here M’ is the mass of the Earth of radius (Re – d)
Assuming the density of Earth ρ to be constant, ρ = `"M"/"V"`
where M is the mass of the Earth and V its volume, thus,
ρ = `"M’"/"V’"`
`"M’"/"V’" = "M"/"V"` and M’ = `"M"/"V""V’"`
M’ = `("M"/(4/3π"R"_"e"^3)) (4/3π("R"_"e" - "d")^3)`
M’ = `"M"/"R"_"e"^3 ("R"_"e" - "d")^3`
g’ = `"G" "M"/"R"_"e"^3 ("R"_"e" - "d")^3 . 1/("R"_"e" - "d")^2`
g’ = `"GM" ("R"_"e" (1 - "d"/"R"_"e"))/("R"_"e"^3)`
g’ = `"GM" ((1 - "d"/"R"_"e"))/"R"_"e"^2`
Thus, g’ = `"g" (1 - "d"/"R"_"e")`
Here also g’ < g. As depth increase, g’ decreases. It is very interesting to know that acceleration due to gravity is maximum on the surface of the Earth but decreases when we go either upward or downward.
APPEARS IN
संबंधित प्रश्न
Assuming the earth to be a sphere of uniform mass density, how much would a body weigh half way down to the centre of the earth if it weighed 250 N on the surface?
An apple falls from a tree. An insect in the apple finds that the earth is falling towards it with an acceleration g. Who exerts the force needed to accelerate the earth with this acceleration g?
Suppose, the acceleration due to gravity at the earth's surface is 10 m s−2 and at the surface of Mars it is 4⋅0 m s−2. A 60 kg passenger goes from the earth to the Mars in a spaceship moving with a constant velocity. Neglect all other objects in the sky. Which part of the following figure best represents the weight (net gravitational force) of the passenger as a function of time?
Find the acceleration due to gravity of the moon at a point 1000 km above the moon's surface. The mass of the moon is 7.4 × 1022 kg and its radius is 1740 km.
Find the height over the Earth's surface at which the weight of a body becomes half of its value at the surface.
Find the acceleration due to gravity in a mine of depth 640 m if the value at the surface is 9.800 m s−2. The radius of the earth is 6400 km.
A body is weighed by a spring balance to be 1.000 kg at the North Pole. How much will it weigh at the equator? Account for the earth's rotation only.
If both the mass and the radius of the earth decrease by 1%, then the value of acceleration due to gravity will
One can easily weigh the earth by calculating the mass of the earth by using the formula:
The percentage decrease in the weight of a rocket, when taken to a height of 32 km above the surface of the earth will, be ______.
(Radius of earth = 6400 km)
