Advertisements
Advertisements
प्रश्न
Derive the time period of the satellite orbiting the Earth.
उत्तर
Time period of the satellite: The distance covered by the satellite during one rotation in its orbit is equal to 2π (RE + h) and time taken for it is the time period, T. Then,
Speed, v = `"Distance travelled"/"Time taken" = (2π ("R"_"E" + "h"))/"T"` ..........(1)
Speed of the satellite, V = `sqrt("GM"_"E"/(("R"_"E" + "h")))`
`sqrt("GM"_"E"/(("R"_"E" + "h"))) = (2π ("R"_"E" + "h"))/"T"`
T = `(2π)/sqrt("GM"_"E") ("R"_"E" + "h")^(3/2)` ............(2)
Squaring both sides of the equation (2) we get,
T2 = `(4π^2)/"GM"_"E" ("R"_"E" + "h")^3`
`(4π^2)/"GM"_"E"` = constant say c
T2 = c(RE + h)3
Equation (3) implies that a satellite orbiting the Earth has the same relation between time and distance as that of Kepler’s law of planetary motion. For a satellite orbiting near the surface of the Earth, h is negligible compared to the radius of the Earth RE. Then,
T2 = `(4π^2)/"GM"_"E" "R"_"E"^3`
T2 = `(4π^2)/(("GM"_"E"/"R"_"E"^2)) "R"_"E"`
T2 = `(4π^2)/"g" "R"_"E"`
Since `"GM"_"E"/"R"_"E"^2` = g
T = `2π sqrt("R"_"E"/"g")`
By substituting the values of RE = 6.4 × 106 m and g = 9.8 ms−2, the orbital time period is obtained as T ≅ 85 minutes.
APPEARS IN
संबंधित प्रश्न
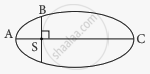
The kinetic energies of a planet in an elliptical orbit about the Sun, at positions A, B and C are KA, KB and KC respectively. AC is the major axis and SB is perpendicular to AC at the position of the Sun S as shown in the figure. Then
If a person moves from Chennai to Trichy, his weight _________.
What are geostationary and polar satellites?
Define weight
Why is there no lunar eclipse and solar eclipse every month?
How will you prove that Earth itself is spinning?
Explain in detail the idea of weightlessness using the lift as an example.
Derive an expression for escape speed.
Derive an expression for the energy of satellite.
Explain in detail the geostationary and polar satellites.
