Advertisements
Advertisements
प्रश्न
f(x) = 9x3 − 3x2 + x − 5, g(x) = \[x - \frac{2}{3}\]
Advertisements
उत्तर
Let us denote the given polynomials as
`f(x) = 9x^2 - 3x^2 + x -5`
`g(x) = x2/3`
We have to find the remainder when f(x) is divided by g(x).
By the remainder theorem, when f(x) is divided by g(x) the remainder is
`f(2/3) = 9(2/3)^2 - 3 (2/3)^2 + (2/3) - 5`
`= 9 xx 8 /27 - 3 xx 4/9 + 2/3 - 5`
` = 8/3 - 4/3 + 2/3 - 5`
`= -3`
Remainder by actual division
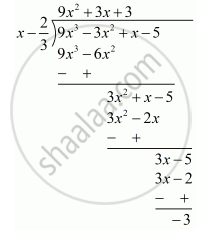
Remainder is −3
APPEARS IN
संबंधित प्रश्न
Write the coefficient of x2 in the following:
`sqrt3x-7`
Identify constant, linear, quadratic and cubic polynomials from the following polynomials:
`r(x)=3x^2+4x^2+5x-7`
If the polynomials ax3 + 3x2 − 13 and 2x3 − 5x + a, when divided by (x − 2) leave the same remainder, find the value of a.
f(x) = x3 −6x2 − 19x + 84, g(x) = x − 7
Show that (x − 2), (x + 3) and (x − 4) are factors of x3 − 3x2 − 10x + 24.
Find the values of a and b, if x2 − 4 is a factor of ax4 + 2x3 − 3x2 + bx − 4.
If x − a is a factor of x3 −3x2a + 2a2x + b, then the value of b is
If x + 2 is a factor of x2 + mx + 14, then m =
If x51 + 51 is divided by x + 1, the remainder is
If (x + 5) and (x – 3) are the factors of ax2 + bx + c, then values of a, b and c are
