Advertisements
Advertisements
प्रश्न
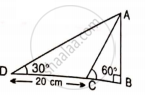
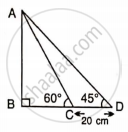
Find AB and BC, if:
उत्तर
Let BC = x m
BD = BC + CD = (x + 20) cm
In ΔABD,
tan 30° = `"AB"/"BD"`
`(1)/(sqrt(3)) = "AB"/(x + 20)`
x + 20 = `sqrt(3)"AB"` ...(1)
In ΔABC
tan 60° = `"AB"/"BC"`
`sqrt(3) = "AB"/x`
x = `"AB"/sqrt(3)` ...(2)
From (1)
`"AB"/sqrt(3) + 20 = sqrt(3)"AB"`
AB + `20sqrt(3)` = 3AB
2AB = `20sqrt(3)`
2AB = `(20sqrt(3))/(2)`
AB = `10sqrt(3)`
AB = 17.32 cm
From (2)
x = `"AB"/sqrt(3)`
x = `(17.32)/sqrt(3)`
x = 10 cm
Therefore BC = x = 10 cm
Therefore, AB = 17.32 cm, BC = 10 cm.
APPEARS IN
संबंधित प्रश्न
Find 'x', if :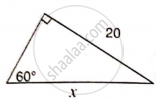
Find angle 'A' if :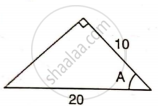
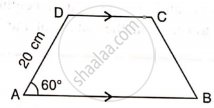
In trapezium ABCD, as shown, AB // DC, AD = DC = BC = 20 cm and A = 60°. Find: distance between AB and DC.
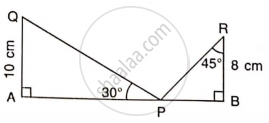
Use the information given to find the length of AB.
In the given figure, AB and EC are parallel to each other. Sides AD and BC are 2 cm each and are perpendicular to AB.
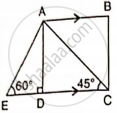
Given that ∠ AED = 60° and ∠ ACD = 45°. Calculate: AB.
In the given figure, AB and EC are parallel to each other. Sides AD and BC are 2 cm each and are perpendicular to AB.

Given that ∠ AED = 60° and ∠ ACD = 45°. Calculate: AE.
In right-angled triangle ABC; ∠ B = 90°. Find the magnitude of angle A, if: AB is √3 times of BC.
A kite is attached to a 100 m long string. Find the greatest height reached by the kite when its string makes an angles of 60° with the level ground.
Find AB and BC, if:
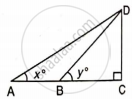
If tan x° = `(5)/(12)`,
tan y° = `(3)/(4)` and AB = 48 m; find the length of CD.