Advertisements
Advertisements
प्रश्न
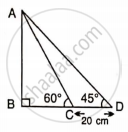
Find AB and BC, if:
उत्तर
Let BC = x m
BD = BC + CD = (x + 20) cm
In ΔABD,
tan 45° = `"AB"/"BD"`
1 = `"AB"/(x + 20)`
x + 20 = AB ...(1)
In ΔABC
tan 60° = `"AB"/"BC"`
`sqrt(3) = "AB"/x`
x = `"AB"/sqrt(3)` ...(2)
From (1)
`"AB"/sqrt(3) + 20 = "AB"`
AB + `20sqrt(3) = sqrt(3)"AB"`
AB`(sqrt(3) -1) = 20sqrt(3)`
AB = `(20sqrt(3))/((sqrt(3) - 1)`
AB = `(20sqrt(3))/((sqrt(3) - 1)) xx ((sqrt(3)+1))/((sqrt(3)+1)`
AB = `(20sqrt(3)(sqrt(3) + 1))/(3 - 1)`
AB = 47.32 cm
From (2)
x = `"AB"/sqrt(3)`
x = `(47.32)/sqrt(3)`
x = 27.32 cm
∴ BC = x = 27.32 cm
Therefore, AB = 47.32 cm, BC = 27.32 cm.
APPEARS IN
संबंधित प्रश्न
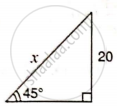
Find 'x', if:
Find angle 'x' if :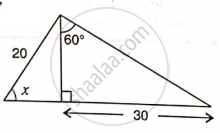
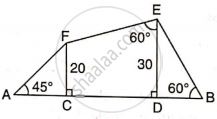
Find AD, if :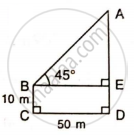
Find AB.
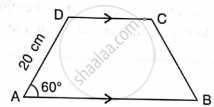
In trapezium ABCD, as shown, AB // DC, AD = DC = BC = 20 cm and ∠ A = 60°. Find: length of AB
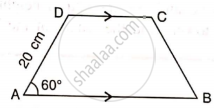
In trapezium ABCD, as shown, AB // DC, AD = DC = BC = 20 cm and A = 60°. Find: distance between AB and DC.
Find: AD
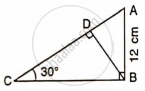
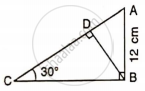
Find: AC
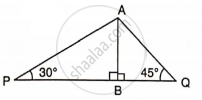
Find PQ, if AB = 150 m, ∠ P = 30° and ∠ Q = 45°.
If tan x° = `(5)/(12)`,
tan y° = `(3)/(4)` and AB = 48 m; find the length of CD.