Advertisements
Advertisements
प्रश्न
Find the angle between the lines whose direction cosines are given by the equations 6mn - 2nl + 5lm = 0, 3l + m + 5n = 0.
उत्तर
Given 6mn - 2nl + 5lm = 0 ....(1)
3l + m + 5n = 0. ...(2)
From (2), m = - 3l - 5n
Putting the value of m in equation (1), we get,
⇒ 6n(- 3l - 5n) - 2nl + 5l(- 3l - 5n) = 0
⇒ - 18nl - 30n2 - 2nl - 15l2 - 25nl = 0
⇒ - 30n2 - 45nl - 15l2 = 0
⇒ 2n2 + 3nl + l2 = 0
⇒ 2n2 + 2nl + nl + l2 = 0
⇒ (2n + l)(n + l) = 0
∴ 2n + l = 0 OR n + l = 0
∴ l = - 2n OR l = - n
∴ l = - 2n
From (2), 3l + m + 5n = 0
∴ - 6n + m + 5n = 0
∴ m = n
i.e. (- 2n, n, n) = (-2, 1, 1)
∴ l = - n
∴- 3n + m + 5n = 0
∴ m = - 2n
i.e. (-n, - 2n, n) = (1, 2, -1)
(a1, b1, c1) = (-2, 1, 1) and (a2, b2, c2) = (1, 2, -1)
cos θ = `|("a"_1"a"_2 + "b"_1"b"_2 + "c"_1"c"_2)/(sqrt("a"_1^2 + "b"_1^2 + "c"_1^2).sqrt ("a"_2^2 + "b"^2_2 + "c"_2^2))|`
`= |((2)(1) + (-1)(2) + (-1)(-1))/(sqrt((2)^2 + 1^2 + 1^2).sqrt(1^2 + 2^2 + (1)^2))|`
`= |(2 - 2 + 1)/(sqrt6.sqrt6)|`
`= |- 1/6| = 1/6`
`θ = "cos"^-1 (1/6)`
APPEARS IN
संबंधित प्रश्न
if `veca = 2hati - hatj - 2hatk " and " vecb = 7hati + 2hatj - 3hatk`, , then express `vecb` in the form of `vecb = vec(b_1) + vec(b_2)`, where `vec(b_1)` is parallel to `veca` and `vec(b_2)` is perpendicular to `veca`
If \[\overrightarrow{a}\], \[\overrightarrow{b}\], \[\overrightarrow{c}\] are the position vectors of the vertices of a triangle, then write the position vector of its centroid.
If \[\overrightarrow{a}\] and \[\overrightarrow{b}\] denote the position vectors of points A and B respectively and C is a point on AB such that 3AC = 2AB, then write the position vector of C.
Write a unit vector making equal acute angles with the coordinates axes.
Find the position vector of the mid-point of the line segment AB, where A is the point (3, 4, −2) and B is the point (1, 2, 4).
Find a unit vector in the direction of \[\overrightarrow{a} = 2 \hat{i} - 3 \hat{j} + 6 \hat{k}\].
Write a unit vector in the direction of \[\overrightarrow{PQ}\], where P and Q are the points (1, 3, 0) and (4, 5, 6) respectively.
If points A (60 \[\hat{i}\] + 3 \[\hat{j}\]), B (40 \[\hat{i}\] − 8 \[\hat{j}\]) and C (a \[\hat{i}\] − 52 \[\hat{j}\]) are collinear, then a is equal to
Let G be the centroid of ∆ ABC. If \[\overrightarrow{AB} = \vec{a,} \overrightarrow{AC} = \vec{b,}\] then the bisector \[\overrightarrow{AG} ,\] in terms of \[\vec{a}\text{ and }\vec{b}\] is
Find the components along the coordinate axes of the position vector of the following point :
Q(–5, 1)
Find the value of λ for which the four points with position vectors `6hat"i" - 7hat"j", 16hat"i" - 19hat"j" - 4hat"k" , lambdahat"j" - 6hat"k" "and" 2hat"i" - 5hat"j" + 10hat"k"` are coplanar.
In the triangle PQR, `bar"PQ" = bar"2a", bar"QR" = bar"2b"`. The midpoint of PR is M. Find the following vectors in terms of `bar"a"` and `bar"b"`:
(i) `bar"PR"` (ii) `bar"PM"` (iii) `bar"QM"`.
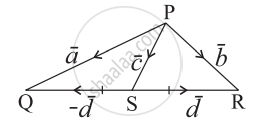
In the given figure express `bar"c"` and `bar"d"` in terms of `bar"a"` and `bar"b"`.
Find the distance from (4, - 2, 6) to each of the following:
(a) The XY-plane
(b) The YZ-plane
(c) The XZ-plane
(d) The X-axis
(e) The Y-axis
(f) The Z-axis.
If `bar"OA" = bar"a" and bar"OB" = bar"b",` then show that the vector along the angle bisector of ∠AOB is given by `bar"d" = lambda(bar"a"/|bar"a"| + bar"b"/|bar"b"|).`
If `bar"a", bar"b", bar"c"` are unit vectors such that `bar"a" + bar"b" + bar"c" = bar0,` then find the value of `bar"a".bar"b" + bar"b".bar"c" + bar"c".bar"a".`
Let bar"b" = 4hat"i" + 3hat"j" and bar"c" be two vectors perpendicular to each other in the XY-plane. Find the vector in the same plane having projection 1 and 2 along bar"b" and bar"c" respectively.
Show that no line in space can make angles `pi/6` and `pi/4` with X-axis and Y-axis.
Find a vector of magnitude 11 in the direction opposite to that of `vec"PQ"` where P and Q are the points (1, 3, 2) and (–1, 0, 8), respectively.
If the points (–1, –1, 2), (2, m, 5) and (3,11, 6) are collinear, find the value of m.
If `vec"a" = 2hat"i" - hat"j" + hat"k", vec"b" = hat"i" + hat"j" - 2hat"k"` and `vec"c" = hat"i" + 3hat"j" - hat"k"`, find `lambda` such that `vec"a"` is perpendicular to `lambdavec"b" + vec"c"`.
The angle between the vectors `hat"i" - hat"j"` and `hat"j" - hat"k"` is ______.
The area of the parallelogram whose adjacent sides are `hat"i" + hat"k"` and `2hat"i" + hat"j" + hat"k"` is ______.
If `|vec"a"|` = 3 and –1 ≤ k ≤ 2, then `|"k"vec"a"|` lies in the interval ______.
If `|vec"a" + vec"b"| = |vec"a" - vec"b"|`, then the vectors `vec"a"` and `vec"b"` are orthogonal.
The formula `(vec"a" + vec"b")^2 = vec"a"^2 + vec"b"^2 + 2vec"a" xx vec"b"` is valid for non-zero vectors `vec"a"` and `vec"b"`
Classify the following measures as scalar and vector.
10-19 coulomb
Let `veca, vecb` and `vecc` be three unit vectors such that `veca xx (vecb xx vecc) = sqrt(3)/2 (vecb + vecc)`. If `vecb` is not parallel to `vecc`, then the angle between `veca` and `vecc` is
Find `|veca xx vecb|`, if `veca = hati - 7hatj + 7hatk` and `vecb = 3hati - 2hatj + 2hatk`
If points P(4, 5, x), Q(3, y, 4) and R(5, 8, 0) are collinear, then the value of x + y is ______.
Check whether the vectors `2hati + 2hatj + 3hatk, - 3hati + 3hatj +2 hatk and 3hati + 4hatk` from a triangle or not.
In the triangle PQR, `bb(bar(PQ) = 2 bara)` and `bb(bar(QR) = 2 barb)`. The mid-point of PR is M. Find the following vectors in terms of `bb(bara and barb)`.
- `bar(PR)`
- `bar(PM)`
- `bar(QM)`
In the triangle PQR, `bar(PQ)=2bara` and `bar(QR)=2barb`. The mid-point of PR is M. Find following vectors in terms of `bara and barb`.
(i) `bar(PR)` (ii) `bar(PM)` (iii) `bar(QM)`
Check whether the vectors `2 hati+2 hatj+3 hatk,-3 hati+3 hatj+2 hatk and 3 hati +4 hatk` form a triangle or not.
Check whether the vectors `2hati + 2hatj +3hatk, - 3hati + 3hatj + 2hatk and 3hati + 4hatk` form a triangle or not.
