Advertisements
Advertisements
प्रश्न
Find the value of λ for which the four points with position vectors `6hat"i" - 7hat"j", 16hat"i" - 19hat"j" - 4hat"k" , lambdahat"j" - 6hat"k" "and" 2hat"i" - 5hat"j" + 10hat"k"` are coplanar.
उत्तर
Let the four points be A, B, C and D, whose position vectors are
P.V. of A = `6hat"i" - 7hat"j"` ,
P.V. of B = `16hat"i" - 19hat"j" - 4hat"k"`
P.V. of C = `lambdahat"j" - 6hat"k"` and
P.V. of D =`2hat"i" - 5hat"j" + 10hat"k"`
∴ `bar"AB" = 10hat"i" - 12hat"j" + 10hat"k"`
`bar"AC" = -6hat"i" + (lambda + 7)hat"j" - 6hat"k"`
`bar"AD" = -4hati + 2hat"j" + 10hat"k"`
Since A,B,C and D are coplanar
`=> bar"AB" , bar"AC" , bar"AD"` are coplanar
`=> bar"AB" bar "AC" bar"AD" = 0`
`=> |(10,-12,-4),(-6,lambda+7,-6),(-4,2,10)| = 0`
`=> 10(10lambda + 70 +12) + 12(-60-24) - 4(-12 + 4lambda + 28)= 0`
`=> 100lambda + 820 - 1008 - 64 - 16lambda = 0`
`=> 84lambda = 252`
`=> lambda = 3`
Henca the value of λ is 3.
APPEARS IN
संबंधित प्रश्न
If \[\vec{a}\], \[\vec{b}\], \[\vec{c}\] represent the sides of a triangle taken in order, then write the value of \[\vec{a} + \vec{b} + \vec{c} .\]
If \[\vec{a}\], \[\vec{b}\], \[\vec{c}\] are the position vectors of the vertices of an equilateral triangle whose orthocentre is at the origin, then write the value of \[\vec{a} + \vec{b} + \vec{c} .\]
If \[\overrightarrow{a} = \hat{i} + \hat{j} , \vec{b} = \hat{j} + \hat{k} \text{ and }\vec{c} = \hat{k} + \hat{i} ,\] write unit vectors parallel to \[\overrightarrow{a} + \overrightarrow{b} - 2 \overrightarrow{c} .\]
If \[\overrightarrow{a} = \hat{i} + \hat{j} , \overrightarrow{b} = \hat{j} + \hat{k} , \overrightarrow{c} = \hat{k} + \hat{i}\], find the unit vector in the direction of \[\overrightarrow{a} + \overrightarrow{b} + \overrightarrow{c}\].
Write a unit vector in the direction of \[\overrightarrow{b} = 2 \hat{i} + \hat{j} + 2 \hat{k}\].
Find a unit vector in the direction of the vector \[\overrightarrow{a} = 3 \hat{i} - 2 \hat{j} + 6 \hat{k}\].
Write the position vector of the point which divides the join of points with position vectors \[3 \overrightarrow{a} - 2 \overrightarrow{b}\text{ and }2 \overrightarrow{a} + 3 \overrightarrow{b}\] in the ratio 2 : 1.
Forces 3 O \[\vec{A}\], 5 O \[\vec{B}\] act along OA and OB. If their resultant passes through C on AB, then
If points A (60 \[\hat{i}\] + 3 \[\hat{j}\]), B (40 \[\hat{i}\] − 8 \[\hat{j}\]) and C (a \[\hat{i}\] − 52 \[\hat{j}\]) are collinear, then a is equal to
Find the components along the coordinate axes of the position vector of the following point :
Q(–5, 1)
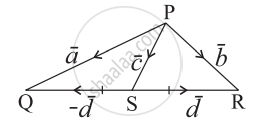
In the given figure express `bar"c"` and `bar"d"` in terms of `bar"a"` and `bar"b"`.
Find the lengths of the sides of the triangle and also determine the type of a triangle:
L (3, -2, -3), M (7, 0, 1), N(1, 2, 1).
Two sides of a parallelogram are `3hat"i" + 4hat"j" - 5hat"k"` and `-2hat"j" + 7hat"k"`. Find the unit vectors parallel to the diagonals.
State whether the expression is meaningful. If not, explain why? If so, state whether it is a vector or a scalar:
`|bar"a"|. (bar"b" + bar"c")`
For any vectors `bar"a", bar"b", bar"c"` show that `(bar"a" + bar"b" + bar"c") xx bar"c" + (bar"a" + bar"b" + bar"c") xx bar"b" + (bar"b" - bar"c") xx bar"a" = 2bar"a" xx bar"c"`
The vector eqliation of line 2x - 2 = 3y + 1 = 6z - 2 is
For any non-zero vectors a and b, [b a × b a] = ?
If the vectors `xhat"i" - 3hat"j" + 7hat"k" and hat"i" + "y"hat"j" - "z"hat"k"` are collinear then the value of `"xy"^2/"z"` is equal.
Classify the following as scalar and vector quantity.
Distance
Classify the following as scalar and vector quantity.
Force
In Figure, identify the following vector.

Equal
Four vectors `veca, vecb, vecc` and `vecx` satisfy the relation `(veca.vecx)vecb = vecc + vecx` where `vecb * veca` ≠ 1. The value of `vecx` in terms of `veca, vecb` and `vecc` is equal to
Check whether the vectors `2hati + 2hatj + 3hatk, -3hati + 3hatj + 2hatk` and `3hati + 4hatk` form a triangle or not.
If `|veca| = 3, |vecb| = sqrt(2)/3` and `veca xx vecb` is a unit vector then the angle between `veca` and `vecb` will be ______.
Evaluate the following.
`int x^3/(sqrt1 + x^4) `dx
Check whether the vectors `2hati + 2hatj + 3hatk, -3hati + 3hatj + 2hatk and 3hati + 4hatk` form a triangle or not.
Check whether the vectors `2hati + 2hatj +3hatk, - 3hati + 3hatj + 2hatk and 3hati + 4hatk` form a triangle or not.
Check whether the vectors `2hati + 2hatj + 3hatk, -3hati + 3hatj + 2hatk and 3hati + 4hatk` form a triangle or not.
Check whether the vectors `2hati + 2hatj +3hatk, - 3hati + 3hatj + 2hatk and 3hati + 4hatk` form a triangle or not.
