Advertisements
Advertisements
प्रश्न
If \[\overrightarrow{a} = \hat{i} + \hat{j} , \overrightarrow{b} = \hat{j} + \hat{k} , \overrightarrow{c} = \hat{k} + \hat{i}\], find the unit vector in the direction of \[\overrightarrow{a} + \overrightarrow{b} + \overrightarrow{c}\].
उत्तर
Let \[\overrightarrow{a} = \hat{i} + \hat{j} , \overrightarrow{b} = \hat{j} + \hat{k} , \overrightarrow{c} = \hat{k} + \hat{i}\]
Then,
\[\overrightarrow{a} + \overrightarrow{b} + \overrightarrow{c} = \hat{i} + \hat{j} + \hat{j} + \hat{k} + \hat{k} + \hat{i} = 2\left( \hat{i} + \hat{j} + \hat{k} \right)\]
∴ \[\left| \overrightarrow{a} + \overrightarrow{b} + \overrightarrow{c} \right| = \sqrt{2^2 + 2^2 + 2^2} = \sqrt{12} = 2\sqrt{3}\] "
Therefore, unit vector in the direction of \[\overrightarrow{a} + \overrightarrow{b} + \overrightarrow{c} = \frac{2\left( \hat{i} + \hat{j} + \hat{k} \right)}{2\sqrt{3}} = \frac{1}{\sqrt{3}}\left( \hat{i} + \hat{j} + \hat{k} \right)\]
APPEARS IN
संबंधित प्रश्न
If \[\vec{a}\] and \[\vec{b}\] represent two adjacent sides of a parallelogram, then write vectors representing its diagonals.
Find the position vector of the mid-point of the line segment AB, where A is the point (3, 4, −2) and B is the point (1, 2, 4).
Find the value of 'p' for which the vectors \[3 \hat{i} + 2 \hat{j} + 9 \hat{k}\] and \[\hat{i} - 2p \hat{j} + 3 \hat{k}\] are parallel.
Write a unit vector in the direction of \[\overrightarrow{PQ}\], where P and Q are the points (1, 3, 0) and (4, 5, 6) respectively.
If \[\vec{a} , \vec{b}\] are the vectors forming consecutive sides of a regular hexagon ABCDEF, then the vector representing side CD is
Forces 3 O \[\vec{A}\], 5 O \[\vec{B}\] act along OA and OB. If their resultant passes through C on AB, then
If O and O' are circumcentre and orthocentre of ∆ ABC, then \[\overrightarrow{OA} + \overrightarrow{OB} + \overrightarrow{OC}\] equals
In Figure, which of the following is not true?
Find the value of λ for which the four points with position vectors `6hat"i" - 7hat"j", 16hat"i" - 19hat"j" - 4hat"k" , lambdahat"j" - 6hat"k" "and" 2hat"i" - 5hat"j" + 10hat"k"` are coplanar.
In the triangle PQR, `bar"PQ" = bar"2a", bar"QR" = bar"2b"`. The midpoint of PR is M. Find the following vectors in terms of `bar"a"` and `bar"b"`:
(i) `bar"PR"` (ii) `bar"PM"` (iii) `bar"QM"`.
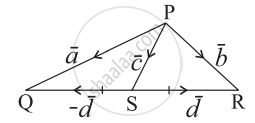
In the given figure express `bar"c"` and `bar"d"` in terms of `bar"a"` and `bar"b"`.
Find the coordinates of the point which is located in the YZ-plane, one unit to the right of the XZ- plane, and six units above the XY-plane.
If P is orthocentre, Q is the circumcentre and G is the centroid of a triangle ABC, then prove that `bar"QP" = 3bar"QG"`.
Express `hat"i" + 4hat"j" - 4hat"k"` as the linear combination of the vectors `2hat"i" - hat"j" + 3hat"k", hat"i" - 2hat"j" + 4hat"k"` and `- hat"i" + 3hat"j" - 5hat"k"`.
Find the angle between the lines whose direction cosines are given by the equations 6mn - 2nl + 5lm = 0, 3l + m + 5n = 0.
Find a unit vector perpendicular to the plane containing the point (a, 0, 0), (0, b, 0) and (0, 0, c). What is the area of the triangle with these vertices?
Find the volume of the parallelopiped spanned by the diagonals of the three faces of a cube of side a that meet at one vertex of the cube.
If the vectors `xhat"i" - 3hat"j" + 7hat"k" and hat"i" + "y"hat"j" - "z"hat"k"` are collinear then the value of `"xy"^2/"z"` is equal.
If the points (–1, –1, 2), (2, m, 5) and (3,11, 6) are collinear, find the value of m.
Find a unit vector in the direction of `vec"PQ"`, where P and Q have co-ordinates (5, 0, 8) and (3, 3, 2), respectively
If `|vec"a" + vec"b"| = |vec"a" - vec"b"|`, then the vectors `vec"a"` and `vec"b"` are orthogonal.
Classify the following as scalar and vector quantity.
Distance
Classify the following as scalar and vector quantity.
Force
In Figure, identify the following vector.

Equal
If `veca ≠ vec(0), veca.vecb = veca.vecc, veca xx vecb = veca xx vecc`, then show that `vecb = vecc`.
Let `veca, vecb` and `vecc` be three unit vectors such that `veca xx (vecb xx vecc) = sqrt(3)/2 (vecb + vecc)`. If `vecb` is not parallel to `vecc`, then the angle between `veca` and `vecc` is
Let `bara, barb` and `barc` be three vectors, then `bara xx (barb xx barc) = (bara xx barb) xx barc` if
Four vectors `veca, vecb, vecc` and `vecx` satisfy the relation `(veca.vecx)vecb = vecc + vecx` where `vecb * veca` ≠ 1. The value of `vecx` in terms of `veca, vecb` and `vecc` is equal to
If `veca = hati - hatj + 7hatk` and `vecb = 5hati - hatj + λhatk`, then find the value of λ so that the vectors `veca + vecb` and `veca - vecb` are orthogonal.
Find the value of λ for which the points (6, – 1, 2), (8, – 7, λ) and (5, 2, 4) are collinear.
Check whether the vectors `2hati + 2 hatj + 3hatk, - 3hati + 3hatj + 2hatk and 3hati + 4hatk` From a triangle or not.
In the triangle PQR, `bar(PQ)=2bara` and `bar(QR)=2barb`. The mid-point of PR is M. Find following vectors in terms of `bara and barb`.
(i) `bar(PR)` (ii) `bar(PM)` (iii) `bar(QM)`
In the triangle PQR, `bar"PQ" = 2 bar" a" and bar"QR" = 2 bar"b"`. The midpoint of PR is M. Find the following vectors in terms of `bar"a"` and `bar"b"`:
(i) `bar"PR"` (ii) `bar"PM"` (iii) `bar"QM"`
Check whether the vectors `2hati + 2hatj + 3hatk, -3hati + 3hatj + 2hatk and 3hati + 4hatk` form a triangle or not.
Check whether the vectors `2hati + 2hatj +3hatk, - 3hati + 3hatj + 2hatk and 3hati + 4hatk` form a triangle or not.
