Advertisements
Advertisements
प्रश्न
Find a unit vector perpendicular to the plane containing the point (a, 0, 0), (0, b, 0) and (0, 0, c). What is the area of the triangle with these vertices?
उत्तर
The position vectors `bar"p", bar"q", bar"r"` of the points A(a, 0, 0), B(0, b, 0), C(0, 0, c) are
`bar"p" = "a"hat"i", bar"q" = "b"hat"j", bar"r" = "c"hat"k"`
`bar"AB" = bar"q" - bar"p" = "b"hat"j" - "a"hat"i" = - "a"hat"j" + "b"hat"j"`
`bar"BC" = bar"r" - bar"q" = "c"hat"k" - "b"hat"j" = - "b"hat"j" + "c"hat"k"`
`bar"AB" xx bar"BC" = |(hat"i",hat"j",hat"k"),(-"a","b",0),(0,-"b","c")|`
`= ("bc" - 0)hat"i" - (- "ac" - 0)hat"j" + ("ab" - 0)hat"k"`
`= "bc"hat"i" + "ac"hat"j" + "ab"hat"k"`
`|bar"AB" xx bar"BC"| = sqrt(("bc")^2 + ("ac")^2 + ("ab")^2)`
`= sqrt("b"^2"c"^2 + "a"^2"c"^2 + "a"^2"b"^2)`
`bar"AB" xx bar"BC"` is perpendicular to the plane containing A, B, C.
∴ the required unit vector
`= (bar"AB" xx bar"BC")/(|bar"AB" xx bar"BC"|) = ("bc"hat"i" + "ca"hat"j" + "ab"hat"k")/sqrt("b"^2"c"^2 + "c"^2"a"^2 + "a"^2"b"^2)`
Area of Δ ABC = `1/2 |bar"AB" xx bar"BC"|`
`= 1/2 sqrt("b"^2"c"^2 + "a"^2"c"^2 + "a"^2"b"^2)` sq.units.
APPEARS IN
संबंधित प्रश्न
If G denotes the centroid of ∆ABC, then write the value of \[\overrightarrow{GA} + \overrightarrow{GB} + \overrightarrow{GC} .\]
If D, E, F are the mid-points of the sides BC, CA and AB respectively of a triangle ABC, write the value of \[\overrightarrow{AD} + \overrightarrow{BE} + \overrightarrow{CF} .\]
Write the position vector of a point dividing the line segment joining points A and B with position vectors \[\vec{a}\] and \[\vec{b}\] externally in the ratio 1 : 4, where \[\overrightarrow{a} = 2 \hat{i} + 3 \hat{j} + 4 \hat{k} \text{ and }\overrightarrow{b} = - \hat{i} + \hat{j} + \hat{k} .\]
If \[\overrightarrow{a} = \hat{i} + \hat{j} , \vec{b} = \hat{j} + \hat{k} \text{ and }\vec{c} = \hat{k} + \hat{i} ,\] write unit vectors parallel to \[\overrightarrow{a} + \overrightarrow{b} - 2 \overrightarrow{c} .\]
Write a unit vector in the direction of \[\overrightarrow{b} = 2 \hat{i} + \hat{j} + 2 \hat{k}\].
Find a unit vector in the direction of the vector \[\overrightarrow{a} = 3 \hat{i} - 2 \hat{j} + 6 \hat{k}\].
If G is the intersection of diagonals of a parallelogram ABCD and O is any point, then \[O \vec{A} + O \vec{B} + O \vec{C} + O \vec{D} =\]
If O and O' are circumcentre and orthocentre of ∆ ABC, then \[\overrightarrow{OA} + \overrightarrow{OB} + \overrightarrow{OC}\] equals
If ABCDEF is a regular hexagon, then \[\overrightarrow{AD} + \overrightarrow{EB} + \overrightarrow{FC}\] equals
If three points A, B and C have position vectors \[\hat{i} + x \hat{j} + 3 \hat{k} , 3 \hat{i} + 4 \hat{j} + 7 \hat{k}\text{ and }y \hat{i} - 2 \hat{j} - 5 \hat{k}\] respectively are collinear, then (x, y) =
ABCDEF is a regular hexagon. Show that `bar"AB" + bar"AC" + bar"AD" + bar"AE" + bar"AF" = 6bar"AO"`, where O is the centre of the hexagon.
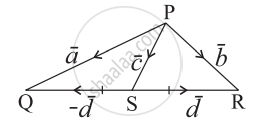
In the given figure express `bar"c"` and `bar"d"` in terms of `bar"a"` and `bar"b"`.
Express `- hat"i" - 3hat"j" + 4hat"k"` as the linear combination of the vectors `2hat"i" + hat"j" - 4hat"k", 2hat"i" - hat"j" + 3hat"k"` and `3hat"i" + hat"j" - 2hat"k"`
If two sides of a triangle are `hat"i" + 2hat"j" and hat"i" + hat"k"`, find the length of the third side.
Find the lengths of the sides of the triangle and also determine the type of a triangle:
L (3, -2, -3), M (7, 0, 1), N(1, 2, 1).
Find the component form of `bar"a"` if it lies in YZ-plane makes 60° with positive Y-axis and `|bar"a"| = 4`.
Find the acute angle between the curves at their points of intersection, y = x2, y = x3.
Show that no line in space can make angles `pi/6` and `pi/4` with X-axis and Y-axis.
State whether the expression is meaningful. If not, explain why? If so, state whether it is a vector or a scalar:
`(bar"a".bar"b") xx (bar"c".bar"d")`
State whether the expression is meaningful. If not, explain why? If so, state whether it is a vector or a scalar:
`(bar"a" xx bar"b").(bar"c"xxbar"d")`
State whether the expression is meaningful. If not, explain why? If so, state whether it is a vector or a scalar:
`(bar"a".bar"b")bar"c"`
The XZ plane divides the line segment joining the points (3, 2, b) and (a, -4, 3) in the ratio ______.
The points A(- a, -b), B (0, 0), C(a, b) and D(a2 , ab) are ______.
If the vectors `xhat"i" - 3hat"j" + 7hat"k" and hat"i" + "y"hat"j" - "z"hat"k"` are collinear then the value of `"xy"^2/"z"` is equal.
Find a vector `vec"r"` of magnitude `3sqrt(2)` units which makes an angle of `pi/4` and `pi/2` with y and z-axes, respectively.
The vector with initial point P (2, –3, 5) and terminal point Q(3, –4, 7) is ______.
If `|vec"a"|` = 8, `|vec"b"|` = 3 and `|vec"a" xx vec"b"|` = 12, then value of `vec"a" * vec"b"` is ______.
Find the unit vector in the direction of the sum of the vectors `vec"a" = 2hat"i" - hat"j" + hat"k"` and `vec"b" = 2hat"j" + hat"k"`.
Classify the following measures as scalar and vector.
10-19 coulomb
Classify the following measures as scalar and vector.
20 m/s2
Let `veca, vecb` and `vecc` be three unit vectors such that `veca xx (vecb xx vecc) = sqrt(3)/2 (vecb + vecc)`. If `vecb` is not parallel to `vecc`, then the angle between `veca` and `vecc` is
The unit vector perpendicular to the vectors `6hati + 2hatj + 3hatk` and `3hati - 6hatj - 2hatk` is
For given vectors, `veca = 2hati - hatj + 2hatk` and `vecb = - hati + hatj - hatk` find the unit vector in the direction of the vector `veca + vecb`.
In the triangle PQR, `bar(PQ) = 2bara` and `bar(QR)=2barb`. The mid-point of PR is M. Find following vectors in terms of `bar a and bar b `.
- `bar("PR")`
- `bar("PM")`
- `bar("QM")`
In the triangle PQR, `bb(bar(PQ) = 2 bara)` and `bb(bar(QR) = 2 barb)`. The mid-point of PR is M. Find the following vectors in terms of `bb(bara and barb)`.
- `bar(PR)`
- `bar(PM)`
- `bar(QM)`
Check whether the vectors `2hati + 2 hatj + 3hatk, - 3hati + 3hatj + 2hatk and 3hati + 4hatk` From a triangle or not.
In the triangle PQR, `bar(PQ)` = 2`bara` and `bar(QR)` = 2`barb`. The midpoint of PR is M. Find the following vectors in terms of `bara` and `barb`.
(i) `bar(PR)` (ii) `bar(PM)` (iii) `bar(QM)`
