Advertisements
Advertisements
प्रश्न
If G is the intersection of diagonals of a parallelogram ABCD and O is any point, then \[O \vec{A} + O \vec{B} + O \vec{C} + O \vec{D} =\]
विकल्प
- \[2 \overrightarrow{OG}\]
- \[4 \overrightarrow{OG}\]
- \[5 \overrightarrow{OG}\]
- \[3 \overrightarrow{OG}\]
उत्तर
Let us consider the point O as origin.
G is the mid point of AC.
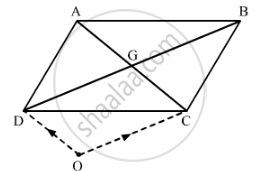
\[\therefore \overrightarrow{OG} = \frac{\overrightarrow{OA} + \overrightarrow{OC}}{2}\]
\[2 \overrightarrow{OG} = \overrightarrow{OA} + \overrightarrow{OC} . . . . . \left( 1 \right)\]
Also, G is the mid point BD
\[\therefore \overrightarrow{OG} = \frac{\overrightarrow{OB} + \overrightarrow{OD}}{2}\]
\[2 \overrightarrow{OG} = \overrightarrow{OB} + \overrightarrow{OD} . . . . . \left( 2 \right)\]
On adding (1) and (2) we get,
\[2 \overrightarrow{OG} + 2 \overrightarrow{OG} = \overrightarrow{OA} + \overrightarrow{OB} + \overrightarrow{OC} + \overrightarrow{OD} \]
\[4 \overrightarrow{OG} = \overrightarrow{OA} + \overrightarrow{OB} + \overrightarrow{OC} + \overrightarrow{OD} \]
\[ \therefore \overrightarrow{OA} + \overrightarrow{OB} + \overrightarrow{OC} + \overrightarrow{OD} = 4 \overrightarrow{OG}\]
APPEARS IN
संबंधित प्रश्न
If \[\overrightarrow{a}\] is a non-zero vector of modulus a and m is a non-zero scalar such that m \[\overrightarrow{a}\] is a unit vector, write the value of m.
In a regular hexagon ABCDEF, A \[\vec{B}\] = a, B \[\vec{C}\] = \[\overrightarrow{b}\text{ and }\overrightarrow{CD} = \vec{c}\].
Then, \[\overrightarrow{AE}\] =
Find the components along the coordinate axes of the position vector of the following point :
S(4, –3)
In Figure, which of the following is not true?
Find a vector in the direction of `bara = hati - 2hatj` that has magnitude 7 units.
Select the correct option from the given alternatives:
The volume of tetrahedron whose vectices are (1,-6,10), (-1, -3, 7), (5, -1, λ) and (7, -4, 7) is 11 cu units, then the value of λ is
Select the correct option from the given alternatives:
The value of `hat"i".(hat"j" xx hat"k") + hat"j".(hat"i" xx hat"k") + hat"k".(hat"i" xx hat"j")` is
If `|bar"a"| = |bar"b"| = 1, bar"a".bar"b" = 0, bar"a" + bar"b" + bar"c" = bar"0", "find" |bar"c"|`.
If `bar"OA" = bar"a" and bar"OB" = bar"b",` then show that the vector along the angle bisector of ∠AOB is given by `bar"d" = lambda(bar"a"/|bar"a"| + bar"b"/|bar"b"|).`
Dot product of a vector with vectors `3hat"i" - 5hat"k", 2hat"i" + 7hat"j" and hat"i" + hat"j" + hat"k"` are respectively -1, 6 and 5. Find the vector.
If a parallelogram is constructed on the vectors `bar"a" = 3bar"p" - bar"q", bar"b" = bar"p" + 3bar"q" and |bar"p"| = |bar"q"| = 2` and angle between `bar"p" and bar"q"` is `pi/3,` and angle between lengths of the sides is `sqrt7 : sqrt13`.
State whether the expression is meaningful. If not, explain why? If so, state whether it is a vector or a scalar:
`bar"a" xx (bar"b".bar"c")`
State whether the expression is meaningful. If not, explain why? If so, state whether it is a vector or a scalar:
`(bar"a".bar"b") xx (bar"c".bar"d")`
State whether the expression is meaningful. If not, explain why? If so, state whether it is a vector or a scalar:
`|bar"a"|(bar"b".bar"c")`
State whether the expression is meaningful. If not, explain why? If so, state whether it is a vector or a scalar:
`|bar"a"|. (bar"b" + bar"c")`
If `bar"a", bar"b", bar"c"` are three non-coplanar vectors show that `(bar"a".(bar"b" xx bar"c"))/((bar"c" xx bar"a").bar"b") + (bar"b".(bar"a" xx bar"c"))/((bar"c" xx bar"a").bar"b") = 0`
lf `overlinea` and `overlineb` be two unit vectors and θ is the angle between them, then `|overlinea - overlineb|` is equal to ______
If `overline"u"` and `overline"v"` are unit vectors and θ is the acute angle between them, then `2overline"u" xx 3overline"v"` is a unit vector for ______
For any vector `overlinex` the value of `(overlinex xx hati)^2 + (overlinex xx hatj)^2 + (overlinex xx hatk)^2` is equal to ______
If the vectors `xhat"i" - 3hat"j" + 7hat"k" and hat"i" + "y"hat"j" - "z"hat"k"` are collinear then the value of `"xy"^2/"z"` is equal.
The vector with initial point P (2, –3, 5) and terminal point Q(3, –4, 7) is ______.
The unit vector perpendicular to the vectors `hat"i" - hat"j"` and `hat"i" + hat"j"` forming a right handed system is ______.
If `vec"a", vec"b", vec"c"` are unit vectors such that `vec"a" + vec"b" + vec"c"` = 0, then the value of `vec"a" * vec"b" + vec"b" * vec"c" + vec"c" * vec"a"` is ______.
If `|vec"a" + vec"b"| = |vec"a" - vec"b"|`, then the vectors `vec"a"` and `vec"b"` are orthogonal.
Classify the following as scalar and vector quantity.
Distance
Classify the following as scalar and vector quantity.
Force
If `veca ≠ vec(0), veca.vecb = veca.vecc, veca xx vecb = veca xx vecc`, then show that `vecb = vecc`.
Let `veca, vecb` and `vecc` be three unit vectors such that `veca xx (vecb xx vecc) = sqrt(3)/2 (vecb + vecc)`. If `vecb` is not parallel to `vecc`, then the angle between `veca` and `vecc` is
The unit vector perpendicular to the vectors `6hati + 2hatj + 3hatk` and `3hati - 6hatj - 2hatk` is
Four vectors `veca, vecb, vecc` and `vecx` satisfy the relation `(veca.vecx)vecb = vecc + vecx` where `vecb * veca` ≠ 1. The value of `vecx` in terms of `veca, vecb` and `vecc` is equal to
Find `|veca xx vecb|`, if `veca = hati - 7hatj + 7hatk` and `vecb = 3hati - 2hatj + 2hatk`
If `veca = hati - hatj + 7hatk` and `vecb = 5hati - hatj + λhatk`, then find the value of λ so that the vectors `veca + vecb` and `veca - vecb` are orthogonal.
Check whether the vectors `2 hati + 2 hatj + 3 hatk, -3 hati + 3 hatj + 2 hatk "and" 3 hati + 4 hatk` from a triangle or not.
In the triangle PQR, `bar(PQ)` = `2bara` and `bar(QR)` = `2barb`. The mid-point of PR is M. Find following vectors in terms of `bara` and `barb`.
(i) `bar(PR)` (ii) `bar(PM)` (iii) `bar(QM)`
If `hata` is unit vector and `(2vecx - 3hata)*(2vecx + 3hata)` = 91, find the value of `|vecx|`.
In the triangle PQR, `bar(PQ)=2bara` and `bar(QR)=2barb`. The mid-point of PR is M. Find following vectors in terms of `bara and barb`.
(i) `bar(PR)` (ii) `bar(PM)` (iii) `bar(QM)`
Check whether the vectors `2 hati+2 hatj+3 hatk,-3 hati+3 hatj+2 hatk and 3 hati +4 hatk` form a triangle or not.
Consider the following statements and choose the correct option:
Statement 1: If `veca` and `vecb` represents two adjacent sides of a parallelogram then the diagonals are represented by `veca + vecb` and `veca - vecb`.
Statement 2: If `veca` and `vecb` represents two diagonals of a parallelogram then the adjacent sides are represented by `2(veca + vecb)` and `2(veca - vecb)`.
Which of the following is correct?
Check whether the vectors `2hati + 2hatj + 3hatk, -3hati + 3hatj + 2hatk and 3hati + 4hatk` form a triangle or not.
