Advertisements
Advertisements
प्रश्न
If G is the intersection of diagonals of a parallelogram ABCD and O is any point, then \[O \vec{A} + O \vec{B} + O \vec{C} + O \vec{D} =\]
पर्याय
- \[2 \overrightarrow{OG}\]
- \[4 \overrightarrow{OG}\]
- \[5 \overrightarrow{OG}\]
- \[3 \overrightarrow{OG}\]
उत्तर
Let us consider the point O as origin.
G is the mid point of AC.
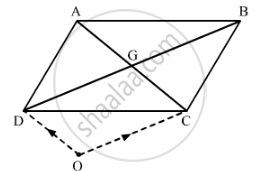
\[\therefore \overrightarrow{OG} = \frac{\overrightarrow{OA} + \overrightarrow{OC}}{2}\]
\[2 \overrightarrow{OG} = \overrightarrow{OA} + \overrightarrow{OC} . . . . . \left( 1 \right)\]
Also, G is the mid point BD
\[\therefore \overrightarrow{OG} = \frac{\overrightarrow{OB} + \overrightarrow{OD}}{2}\]
\[2 \overrightarrow{OG} = \overrightarrow{OB} + \overrightarrow{OD} . . . . . \left( 2 \right)\]
On adding (1) and (2) we get,
\[2 \overrightarrow{OG} + 2 \overrightarrow{OG} = \overrightarrow{OA} + \overrightarrow{OB} + \overrightarrow{OC} + \overrightarrow{OD} \]
\[4 \overrightarrow{OG} = \overrightarrow{OA} + \overrightarrow{OB} + \overrightarrow{OC} + \overrightarrow{OD} \]
\[ \therefore \overrightarrow{OA} + \overrightarrow{OB} + \overrightarrow{OC} + \overrightarrow{OD} = 4 \overrightarrow{OG}\]
APPEARS IN
संबंधित प्रश्न
If `veca=xhati+2hatj-zhatk and vecb=3hati-yhatj+hatk` are two equal vectors ,then write the value of x+y+z
If \[\overrightarrow{a}\], \[\overrightarrow{b}\], \[\overrightarrow{c}\] are the position vectors of the vertices of a triangle, then write the position vector of its centroid.
If G denotes the centroid of ∆ABC, then write the value of \[\overrightarrow{GA} + \overrightarrow{GB} + \overrightarrow{GC} .\]
Write a unit vector making equal acute angles with the coordinates axes.
Write a unit vector in the direction of \[\overrightarrow{a} = 3 \hat{i} + 2 \hat{j} + 6 \hat{k} .\]
If \[\overrightarrow{a} = \hat{i} + 2 \hat{j} - 3 \hat{k} \text{ and }\overrightarrow{b} = 2 \hat{i} + 4 \hat{j} + 9 \hat{k} ,\] find a unit vector parallel to \[\overrightarrow{a} + \overrightarrow{b}\].
If \[\vec{a} , \vec{b} , \vec{c}\] are three non-zero vectors, no two of which are collinear and the vector \[\vec{a} + \vec{b}\] is collinear with \[\vec{c} , \vec{b} + \vec{c}\] is collinear with \[\vec{a} ,\] then \[\vec{a} + \vec{b} + \vec{c} =\]
In a regular hexagon ABCDEF, A \[\vec{B}\] = a, B \[\vec{C}\] = \[\overrightarrow{b}\text{ and }\overrightarrow{CD} = \vec{c}\].
Then, \[\overrightarrow{AE}\] =
The position vectors of the points A, B, C are \[2 \hat{i} + \hat{j} - \hat{k} , 3 \hat{i} - 2 \hat{j} + \hat{k}\text{ and }\hat{i} + 4 \hat{j} - 3 \hat{k}\] respectively.
These points
If \[\vec{a}\text{ and }\vec{b}\] are two collinear vectors, then which of the following are incorrect?
Find the vector equation of the plane through the line of intersection of the planes x + y + z = 1 and 2x + 3y + 4z = 5 which is perpendicular to the plane x – y + z = 0. Hence find whether the plane thus obtained contains the line \[\frac{x + 2}{5} = \frac{y - 3}{4} = \frac{z}{5}\] or not.
Find the components along the coordinate axes of the position vector of the following point :
P(3, 2)
Find the components along the coordinate axes of the position vector of the following point :
Q(–5, 1)
Find the position vector of the mid-point of the vector joining the points
ABCDEF is a regular hexagon. Show that `bar"AB" + bar"AC" + bar"AD" + bar"AE" + bar"AF" = 6bar"AO"`, where O is the centre of the hexagon.
Find the coordinates of the point which is located three units behind the YZ-plane, four units to the right of XZ-plane, and five units above the XY-plane.
If `|bara|` = 3, `|barb|` = 5, `|barc|` = 7 and `bara + barb + barc = bar0`, then the angle between `bara` and `barb` is ______.
Select the correct option from the given alternatives:
The volume of tetrahedron whose vectices are (1,-6,10), (-1, -3, 7), (5, -1, λ) and (7, -4, 7) is 11 cu units, then the value of λ is
Select the correct option from the given alternatives:
Let a, b, c be distinct non-negative numbers. If the vectors `"a"hat"i" + "a"hat"j" + "c"hat"k" , hat"i" + hat"k" "and" "c"hat"i" + "c"hat"j" + "b"hat"k"` lie in a plane, then c is
Dot product of a vector with vectors `3hat"i" - 5hat"k", 2hat"i" + 7hat"j" and hat"i" + hat"j" + hat"k"` are respectively -1, 6 and 5. Find the vector.
If the vectors `overlinea = 2hati - qhatj + 3hatk` and `overlineb = 4hati - 5hatj + 6hatk` are collinear, then the value of q is ______
Find the unit vector in the direction of the sum of the vectors `vec"a" = 2hat"i" - hat"j" + 2hat"k"` and `vec"b" = -hat"i" + hat"j" + 3hat"k"`.
If the points (–1, –1, 2), (2, m, 5) and (3,11, 6) are collinear, find the value of m.
If `veca` and `vecb` are unit vectors, then what is the angle between `veca` and `vecb` for `sqrt(3) veca - vecb` to be a unit vector?
Classify the following measures as scalar and vector.
40°
Classify the following measures as scalar and vector.
10-19 coulomb
Classify the following measures as scalar and vector.
20 m/s2
Classify the following as scalar and vector quantity.
Velocity
Classify the following as scalar and vector quantity.
Work done
If points P(4, 5, x), Q(3, y, 4) and R(5, 8, 0) are collinear, then the value of x + y is ______.
In the triangle PQR, `bb(bar(PQ) = 2 bara)` and `bb(bar(QR) = 2 barb)`. The mid-point of PR is M. Find the following vectors in terms of `bb(bara and barb)`.
- `bar(PR)`
- `bar(PM)`
- `bar(QM)`
Check whether the vectors `2hati+2hatj+3hatk,-3hati+3hatj+2hatk` and `3hati+4hatk` form a triangle or not.
Consider the following statements and choose the correct option:
Statement 1: If `veca` and `vecb` represents two adjacent sides of a parallelogram then the diagonals are represented by `veca + vecb` and `veca - vecb`.
Statement 2: If `veca` and `vecb` represents two diagonals of a parallelogram then the adjacent sides are represented by `2(veca + vecb)` and `2(veca - vecb)`.
Which of the following is correct?
Check whether the vectors `2hati + 2hatj + 3hatk, -3hati + 3hatj + 2hatk and 3hati + 4hatk` form a triangle or not.
In the triangle PQR, `bar(PQ)` = 2`bara` and `bar(QR)` = 2`barb`. The midpoint of PR is M. Find the following vectors in terms of `bara` and `barb`.
(i) `bar(PR)` (ii) `bar(PM)` (iii) `bar(QM)`
