Advertisements
Advertisements
प्रश्न
If \[\vec{a}\text{ and }\vec{b}\] are two collinear vectors, then which of the following are incorrect?
पर्याय
\[\vec{b} = \lambda \vec{a}\] for some scalar λ
- \[\vec{a} = \pm \vec{b}\]
the respective components of \[\vec{a}\text{ and }\vec{b}\] are proportional
both the vectors \[\vec{a}\text{ and }\vec{b}\] have the same direction but different magnitudes
उत्तर
both the vectors \[\vec{a}\text{ and }\vec{b}\] have the same direction but different magnitudes
If \[\vec{a}\text{ and }\vec{b}\] are collinear vectors, then they are paprallel. Therefore, we have \[\vec{b} = \lambda \vec{a}\] , for some scalar \[\lambda\]
If \[\lambda = \pm 1\]
\[\Rightarrow \vec{a} = \pm \vec{b} .\]
If \[b = b_1 \hat{i} + b_2 \hat{j} + b_3 \hat{k}\] and \[\vec{a} = a_1 \hat{i} + a_2 \hat{j} + a_3 \hat{k}\].
Then,
\[\vec{b} = \lambda \vec{a} . \]
\[ \Rightarrow b_1 \hat{i} + b_2 \hat{j} + b_3 \hat{k} = \lambda \left( a_1 \hat{i} + a_2 \hat{j} + a_3 \hat{k} \right) . \]
\[ \Rightarrow b_1 \hat{i} + b_2 \hat{j} + b_3 \hat{k} = \left( \lambda a_1 \right) \hat{i} + \left( \lambda a_2 \right) \hat{j} + \left( \lambda a_3 \right) \hat{k} . \]
\[ \Rightarrow b_1 = \lambda a_1 , b_2 = \lambda a_2 , b_3 = \lambda a_3 . \]
\[ \Rightarrow \frac{b_1}{a_1} = \frac{b_2}{a_2} = \frac{b_3}{a_3} = \lambda .\]
Thus, the respective components of \[\vec{a}\text{ and }\vec{b}\] can have different directions. Hence, the statement given in (d) is incorrect.
APPEARS IN
संबंधित प्रश्न
If \[\overrightarrow{a}\], \[\overrightarrow{b}\], \[\overrightarrow{c}\] are the position vectors of the vertices of a triangle, then write the position vector of its centroid.
If \[\vec{a}\], \[\vec{b}\], \[\vec{c}\] are the position vectors of the vertices of an equilateral triangle whose orthocentre is at the origin, then write the value of \[\vec{a} + \vec{b} + \vec{c} .\]
Write the position vector of a point dividing the line segment joining points A and B with position vectors \[\vec{a}\] and \[\vec{b}\] externally in the ratio 1 : 4, where \[\overrightarrow{a} = 2 \hat{i} + 3 \hat{j} + 4 \hat{k} \text{ and }\overrightarrow{b} = - \hat{i} + \hat{j} + \hat{k} .\]
If \[\overrightarrow{a} = \hat{i} + \hat{j} , \overrightarrow{b} = \hat{j} + \hat{k} , \overrightarrow{c} = \hat{k} + \hat{i}\], find the unit vector in the direction of \[\overrightarrow{a} + \overrightarrow{b} + \overrightarrow{c}\].
Find the position vector of the mid-point of the line segment AB, where A is the point (3, 4, −2) and B is the point (1, 2, 4).
If \[\vec{a}\], \[\vec{b}\], \[\vec{c}\] and \[\vec{d}\] are the position vectors of points A, B, C, D such that no three of them are collinear and \[\vec{a} + \vec{c} = \vec{b} + \vec{d} ,\] then ABCD is a
Find the components along the coordinate axes of the position vector of the following point :
R(–11, –9)
Find the position vector of the mid-point of the vector joining the points
OABCDE is a regular hexagon. The points A and B have position vectors `bar"a"` and `bar"b"` respectively referred to the origin O. Find, in terms of `bar"a"` and `bar"b"` the position vectors of C, D and E.
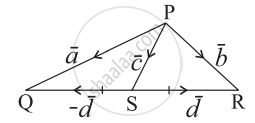
In the given figure express `bar"c"` and `bar"d"` in terms of `bar"a"` and `bar"b"`.
Find a vector in the direction of `bara = hati - 2hatj` that has magnitude 7 units.
Find the coordinates of the point which is located three units behind the YZ-plane, four units to the right of XZ-plane, and five units above the XY-plane.
Select the correct option from the given alternatives:
If `bar"a" "and" bar"b"` are unit vectors, then what is the angle between `bar"a"` and `bar"b"` for `sqrt3bar"a" - bar"b"` to be a unit vector?
Select the correct option from the given alternatives:
Let a, b, c be distinct non-negative numbers. If the vectors `"a"hat"i" + "a"hat"j" + "c"hat"k" , hat"i" + hat"k" "and" "c"hat"i" + "c"hat"j" + "b"hat"k"` lie in a plane, then c is
ABCD is a parallelogram. E, F are the midpoints of BC and CD respectively. AE, AF meet the diagonal BD at Q and P respectively. Show that P and Q trisect DB.
If P is orthocentre, Q is the circumcentre and G is the centroid of a triangle ABC, then prove that `bar"QP" = 3bar"QG"`.
Find a unit vector perpendicular to the plane containing the point (a, 0, 0), (0, b, 0) and (0, 0, c). What is the area of the triangle with these vertices?
State whether the expression is meaningful. If not, explain why? If so, state whether it is a vector or a scalar:
`(bar"a".bar"b") xx (bar"c".bar"d")`
For any non zero vector, a, b, c a · ((b + c) × (a + b + c)] = ______.
If the points (–1, –1, 2), (2, m, 5) and (3,11, 6) are collinear, find the value of m.
The unit vector perpendicular to the vectors `hat"i" - hat"j"` and `hat"i" + hat"j"` forming a right handed system is ______.
If `|vec"a"|` = 3 and –1 ≤ k ≤ 2, then `|"k"vec"a"|` lies in the interval ______.
Find a unit vector in the direction of `vec"PQ"`, where P and Q have co-ordinates (5, 0, 8) and (3, 3, 2), respectively
If `vec"a", vec"b", vec"c"` determine the vertices of a triangle, show that `1/2[vec"b" xx vec"c" + vec"c" xx vec"a" + vec"a" xx vec"b"]` gives the vector area of the triangle. Hence deduce the condition that the three points `vec"a", vec"b", vec"c"` are collinear. Also find the unit vector normal to the plane of the triangle.
The vector `vec"a" + vec"b"` bisects the angle between the non-collinear vectors `vec"a"` and `vec"b"` if ______.
If `vec"a"` is any non-zero vector, then `(vec"a" .hat"i")hat"i" + (vec"a".hat"j")hat"j" + (vec"a".hat"k")hat"k"` equals ______.
Classify the following measures as scalar and vector.
10-19 coulomb
Classify the following as scalar and vector quantity.
Velocity
Let the vectors `vec(a)` such `vec(b)` that `|veca|` = 3 and `|vecb| = sqrt(2)/3`, then `veca xx vecb` is a unit vector if the angle between `veca` and `vecb` is
If `veca = hati - hatj + 7hatk` and `vecb = 5hati - hatj + λhatk`, then find the value of λ so that the vectors `veca + vecb` and `veca - vecb` are orthogonal.
In the triangle PQR, `bar"PQ" = 2 bar" a" and bar"QR" = 2 bar"b"`. The midpoint of PR is M. Find the following vectors in terms of `bar"a"` and `bar"b"`:
(i) `bar"PR"` (ii) `bar"PM"` (iii) `bar"QM"`
Check whether the vectors `2hati+2hatj+3hatk,-3hati+3hatj+2hatk` and `3hati+4hatk` form a triangle or not.
Check whether the vectors `2hati + 2hatj + 3hatk, -3hati + 3hatj + 2hatk and 3hati + 4hatk` form a triangle or not.
In the triangle PQR, `bar(PQ) = 2bara and bar(QR) = 2barb`. The mid-point of PR is M. Find the following vectors in terms of `bara and barb`.
- `bar(PR)`
- `bar(PM)`
- `bar(QM)`
Check whether the vectors `2hati + 2hatj +3hatk, - 3hati + 3hatj + 2hatk and 3hati + 4hatk` form a triangle or not.
Consider the following statements and choose the correct option:
Statement 1: If `veca` and `vecb` represents two adjacent sides of a parallelogram then the diagonals are represented by `veca + vecb` and `veca - vecb`.
Statement 2: If `veca` and `vecb` represents two diagonals of a parallelogram then the adjacent sides are represented by `2(veca + vecb)` and `2(veca - vecb)`.
Which of the following is correct?
