Advertisements
Advertisements
प्रश्न
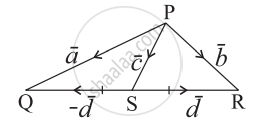
In the given figure express `bar"c"` and `bar"d"` in terms of `bar"a"` and `bar"b"`.
उत्तर
`bar"PQ" = bar"PS" + bar"SQ"`
∴ `bar"a" = bar"c" - bar"d"` ...(1)
`bar"PR" = bar"PS" + bar"SR"`
∴ `bar"b" = bar"c" + bar"d"` ....(2)
Adding equations (1) and (2), we get,
`bar"a" + bar"b" = (bar"c" - bar"d") + (bar"c" + bar"d") = 2bar"c"`
∴ `bar"c" = 1/2 (bar"a" + bar"b")`
∴ `bar"c" = 1/2 bar"a" + 1/2bar"b"`
Substituting for `bar"c"` in (2), we get,
∴ `bar"b" = bar"c" + bar"d"`
∴ `bar"d" = bar"b" − bar"c"`
∴ `bar"d" = bar"b" − 1/2 (bar"a" + bar"b")`
∴ `bar"d" = (2bar"b" − (bar"a" + bar"b"))/2`
∴ `bar"d" = (2bar"b" − bar"a" − bar"b")/2`
∴ `bar"d" = (bar"b" − bar"a")/2`
∴ `bar"d" = 1/2 (bar"b" − bar"a")`
∴ `bar"d" = 1/2bar"b" - 1/2bar"a"`
Hence, `bar"c" = 1/2 bar"a" + 1/2bar"b"` and `bar"d" = 1/2bar"b" - 1/2bar"a"`.
APPEARS IN
संबंधित प्रश्न
If \[\overrightarrow{a}\], \[\overrightarrow{b}\], \[\overrightarrow{c}\] are the position vectors of the vertices of a triangle, then write the position vector of its centroid.
Write a unit vector in the direction of \[\overrightarrow{b} = 2 \hat{i} + \hat{j} + 2 \hat{k}\].
Find a unit vector in the direction of the vector \[\overrightarrow{a} = 3 \hat{i} - 2 \hat{j} + 6 \hat{k}\].
If \[\vec{a} , \vec{b}\] are the vectors forming consecutive sides of a regular hexagon ABCDEF, then the vector representing side CD is
If ABCDEF is a regular hexagon, then \[\overrightarrow{AD} + \overrightarrow{EB} + \overrightarrow{FC}\] equals
If three points A, B and C have position vectors \[\hat{i} + x \hat{j} + 3 \hat{k} , 3 \hat{i} + 4 \hat{j} + 7 \hat{k}\text{ and }y \hat{i} - 2 \hat{j} - 5 \hat{k}\] respectively are collinear, then (x, y) =
If \[\vec{a}\text{ and }\vec{b}\] are two collinear vectors, then which of the following are incorrect?
Find the components along the coordinate axes of the position vector of the following point :
Q(–5, 1)
Find the components along the coordinate axes of the position vector of the following point :
S(4, –3)
Find a unit vector perpendicular to each of the vectors `veca + vecb "and" veca - vecb "where" veca = 3hati + 2hatj + 2hatk and vecb = i + 2hatj - 2hatk`
In the triangle PQR, `bar"PQ" = bar"2a", bar"QR" = bar"2b"`. The midpoint of PR is M. Find the following vectors in terms of `bar"a"` and `bar"b"`:
(i) `bar"PR"` (ii) `bar"PM"` (iii) `bar"QM"`.
Find a vector in the direction of `bara = hati - 2hatj` that has magnitude 7 units.
Find the distance from (4, - 2, 6) to each of the following:
(a) The XY-plane
(b) The YZ-plane
(c) The XZ-plane
(d) The X-axis
(e) The Y-axis
(f) The Z-axis.
Select the correct option from the given alternatives:
Let a, b, c be distinct non-negative numbers. If the vectors `"a"hat"i" + "a"hat"j" + "c"hat"k" , hat"i" + hat"k" "and" "c"hat"i" + "c"hat"j" + "b"hat"k"` lie in a plane, then c is
Find the lengths of the sides of the triangle and also determine the type of a triangle:
L (3, -2, -3), M (7, 0, 1), N(1, 2, 1).
Find the component form of `bar"a"` if it lies in YZ-plane makes 60° with positive Y-axis and `|bar"a"| = 4`.
If `bar"OA" = bar"a" and bar"OB" = bar"b",` then show that the vector along the angle bisector of ∠AOB is given by `bar"d" = lambda(bar"a"/|bar"a"| + bar"b"/|bar"b"|).`
Express the vector `bar"a" = 5hat"i" - 2hat"j" + 5hat"k"` as a sum of two vectors such that one is parallel to the vector `bar"b" = 3hat"i" + hat"k"` and other is perpendicular to `bar"b"`.
Find two unit vectors each of which makes equal angles with bar"u", bar"v" and bar"w" where bar"u" = 2hat"i" + hat"j" - 2hat"k", bar"v" = hat"i" + 2hat"j" - 2hat"k", bar"w" = 2hat"i" - 2hat"j" + hat"k".
Express `hat"i" + 4hat"j" - 4hat"k"` as the linear combination of the vectors `2hat"i" - hat"j" + 3hat"k", hat"i" - 2hat"j" + 4hat"k"` and `- hat"i" + 3hat"j" - 5hat"k"`.
Find the angle between the lines whose direction cosines are given by the equations 6mn - 2nl + 5lm = 0, 3l + m + 5n = 0.
State whether the expression is meaningful. If not, explain why? If so, state whether it is a vector or a scalar:
`(bar"a" xx bar"b").(bar"c"xxbar"d")`
The points A(- a, -b), B (0, 0), C(a, b) and D(a2 , ab) are ______.
If the vectors `overlinea = 2hati - qhatj + 3hatk` and `overlineb = 4hati - 5hatj + 6hatk` are collinear, then the value of q is ______
Find a vector of magnitude 11 in the direction opposite to that of `vec"PQ"` where P and Q are the points (1, 3, 2) and (–1, 0, 8), respectively.
If `vec"a" = 2hat"i" - hat"j" + hat"k", vec"b" = hat"i" + hat"j" - 2hat"k"` and `vec"c" = hat"i" + 3hat"j" - hat"k"`, find `lambda` such that `vec"a"` is perpendicular to `lambdavec"b" + vec"c"`.
The vector with initial point P (2, –3, 5) and terminal point Q(3, –4, 7) is ______.
If `|vec"a"|` = 8, `|vec"b"|` = 3 and `|vec"a" xx vec"b"|` = 12, then value of `vec"a" * vec"b"` is ______.
The vector `vec"a" + vec"b"` bisects the angle between the non-collinear vectors `vec"a"` and `vec"b"` if ______.
Let `veca, vecb` and `vecc` be three unit vectors such that `veca xx (vecb xx vecc) = sqrt(3)/2 (vecb + vecc)`. If `vecb` is not parallel to `vecc`, then the angle between `veca` and `vecc` is
If points P(4, 5, x), Q(3, y, 4) and R(5, 8, 0) are collinear, then the value of x + y is ______.
Unit vector along `vec(PQ)`, where coordinates of P and Q respectively are (2, 1, – 1) and (4, 4, – 7), is ______.
Check whether the vectors `2hati + 2hatj + 3hatk, - 3hati + 3hatj +2 hatk and 3hati + 4hatk` from a triangle or not.
Check whether the vectors `2hati + 2hatj + 3hatk, -3hati + 3hatj + 2hatk` and `3hati + 4hatk` form a triangle or not.
Check whether the vectors `2hati + 2 hatj + 3hatk, - 3hati + 3hatj + 2hatk and 3hati + 4hatk` From a triangle or not.
Check whether the vectors `2hati + 2hatj + 3hatk, -3hati + 3hatj + 2hatk and 3hati + 4hatk` form a triangle or not.
