Advertisements
Advertisements
प्रश्न
If \[\overrightarrow{a} = \hat{i} + 2 \hat{j} - 3 \hat{k} \text{ and }\overrightarrow{b} = 2 \hat{i} + 4 \hat{j} + 9 \hat{k} ,\] find a unit vector parallel to \[\overrightarrow{a} + \overrightarrow{b}\].
उत्तर
Given: \[\overrightarrow{a} = \hat{i} + 2 \hat{j} - 3 \hat{k} , \overrightarrow{b} = 2 \hat{i} + 4 \hat{j} + 9 \hat{k} \]
\[\text{ Now, }\overrightarrow{a} + \overrightarrow{b} = 3 \hat{i} + 6 \hat{j} + 6 \hat{k} \]
\[\left| \overrightarrow{a} + \overrightarrow{b} \right| = \sqrt{3^2 + 6^2 + 6^2} = \sqrt{9 + 36 + 36} = \sqrt{81} = 9\]
Unit vector parallel to \[\overrightarrow{a} + \overrightarrow{b} = \frac{\overrightarrow{a} + \overrightarrow{b}}{\left| \overrightarrow{a} + \overrightarrow{b} \right|} = \frac{3 \hat{i} + 6 \hat{j} + 6 \hat{k}}{9} = \frac{1}{9} \times 3\left( \hat{i} + 2 \hat{j} + 2 \hat{k} \right) = \frac{1}{3}\left( \hat{i} + 2 \hat{j} + 2 \hat{k} \right)\]
APPEARS IN
संबंधित प्रश्न
If \[\overrightarrow{a} = \hat{i} + \hat{j} , \overrightarrow{b} = \hat{j} + \hat{k} , \overrightarrow{c} = \hat{k} + \hat{i}\], find the unit vector in the direction of \[\overrightarrow{a} + \overrightarrow{b} + \overrightarrow{c}\].
Write a unit vector in the direction of \[\overrightarrow{PQ}\], where P and Q are the points (1, 3, 0) and (4, 5, 6) respectively.
Write the position vector of the point which divides the join of points with position vectors \[3 \overrightarrow{a} - 2 \overrightarrow{b}\text{ and }2 \overrightarrow{a} + 3 \overrightarrow{b}\] in the ratio 2 : 1.
If \[\vec{a} , \vec{b} , \vec{c}\] are three non-zero vectors, no two of which are collinear and the vector \[\vec{a} + \vec{b}\] is collinear with \[\vec{c} , \vec{b} + \vec{c}\] is collinear with \[\vec{a} ,\] then \[\vec{a} + \vec{b} + \vec{c} =\]
If O and O' are circumcentre and orthocentre of ∆ ABC, then \[\overrightarrow{OA} + \overrightarrow{OB} + \overrightarrow{OC}\] equals
If ABCDEF is a regular hexagon, then \[\overrightarrow{AD} + \overrightarrow{EB} + \overrightarrow{FC}\] equals
If three points A, B and C have position vectors \[\hat{i} + x \hat{j} + 3 \hat{k} , 3 \hat{i} + 4 \hat{j} + 7 \hat{k}\text{ and }y \hat{i} - 2 \hat{j} - 5 \hat{k}\] respectively are collinear, then (x, y) =
Find the components along the coordinate axes of the position vector of the following point :
S(4, –3)
ABCDEF is a regular hexagon. Show that `bar"AB" + bar"AC" + bar"AD" + bar"AE" + bar"AF" = 6bar"AO"`, where O is the centre of the hexagon.
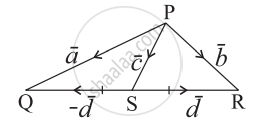
In the given figure express `bar"c"` and `bar"d"` in terms of `bar"a"` and `bar"b"`.
Find the distance from (4, - 2, 6) to each of the following:
(a) The XY-plane
(b) The YZ-plane
(c) The XZ-plane
(d) The X-axis
(e) The Y-axis
(f) The Z-axis.
Find the coordinates of the point which is located three units behind the YZ-plane, four units to the right of XZ-plane, and five units above the XY-plane.
Select the correct option from the given alternatives:
If l, m, n are direction cosines of a line then `"l"hat
"i" + "m"hat"j" + "n"hat"k"` is ______
Select the correct option from the given alternatives:
The value of `hat"i".(hat"j" xx hat"k") + hat"j".(hat"i" xx hat"k") + hat"k".(hat"i" xx hat"j")` is
If two sides of a triangle are `hat"i" + 2hat"j" and hat"i" + hat"k"`, find the length of the third side.
Find the unit vectors that are parallel to the tangent line to the parabola y = x2 at the point (2, 4).
If `bar"a", bar"b", bar"c"` are unit vectors such that `bar"a" + bar"b" + bar"c" = bar0,` then find the value of `bar"a".bar"b" + bar"b".bar"c" + bar"c".bar"a".`
State whether the expression is meaningful. If not, explain why? If so, state whether it is a vector or a scalar:
`bar"a" xx (bar"b".bar"c")`
State whether the expression is meaningful. If not, explain why? If so, state whether it is a vector or a scalar:
`(bar"a".bar"b") xx (bar"c".bar"d")`
State whether the expression is meaningful. If not, explain why? If so, state whether it is a vector or a scalar:
`(bar"a" xx bar"b").(bar"c"xxbar"d")`
The XZ plane divides the line segment joining the points (3, 2, b) and (a, -4, 3) in the ratio ______.
The points A(- a, -b), B (0, 0), C(a, b) and D(a2 , ab) are ______.
lf `overlinea` and `overlineb` be two unit vectors and θ is the angle between them, then `|overlinea - overlineb|` is equal to ______
Find a vector of magnitude 11 in the direction opposite to that of `vec"PQ"` where P and Q are the points (1, 3, 2) and (–1, 0, 8), respectively.
If `vec"a" = hat"i" + hat"j" + 2hat"k"` and `vec"b" = 2hat"i" + hat"j" - 2hat"k"`, find the unit vector in the direction of `6vec"b"`
Using vectors, find the value of k such that the points (k, – 10, 3), (1, –1, 3) and (3, 5, 3) are collinear.
The formula `(vec"a" + vec"b")^2 = vec"a"^2 + vec"b"^2 + 2vec"a" xx vec"b"` is valid for non-zero vectors `vec"a"` and `vec"b"`
Classify the following measures as scalar and vector.
2 meters north-west
Classify the following measures as scalar and vector.
20 m/s2
Classify the following as scalar and vector quantity.
Force
The unit vector perpendicular to the vectors `6hati + 2hatj + 3hatk` and `3hati - 6hatj - 2hatk` is
For given vectors, `veca = 2hati - hatj + 2hatk` and `vecb = - hati + hatj - hatk` find the unit vector in the direction of the vector `veca + vecb`.
If `veca` and `vecb` are two collinear vectors then which of the following are incorrect.
Let the vectors `vec(a)` such `vec(b)` that `|veca|` = 3 and `|vecb| = sqrt(2)/3`, then `veca xx vecb` is a unit vector if the angle between `veca` and `vecb` is
In the triangle PQR, `bar("P""Q")`= `2 bar"a"` and `bar ("QR")` = `2 barb`.The mid - point of PR is M. Find following vector in term of `bar a ` and `barb.`
- `bar("P""R")`
- `bar("P""M")`
- `bar("Q""M")`
If A(1, 2, – 3) and B(– 1, – 2, 1) are the end points of a vector `vec("AB")` then find the unit vector in the direction of `vec("AB")`.
Check whether the vectors `2hati+2hatj+3hatk,-3hati+3hatj+2hatk` and `3hati+4hatk` form a triangle or not.
Consider the following statements and choose the correct option:
Statement 1: If `veca` and `vecb` represents two adjacent sides of a parallelogram then the diagonals are represented by `veca + vecb` and `veca - vecb`.
Statement 2: If `veca` and `vecb` represents two diagonals of a parallelogram then the adjacent sides are represented by `2(veca + vecb)` and `2(veca - vecb)`.
Which of the following is correct?
